
【题目】如图,在△ABC中,∠ACB=90°,∠A=30°,AB的垂直平分线分别交AB和AC于点D,E.

(1)求证:AE=2CE;
(2)连接CD,请判断△BCD的形状,并说明理由.
【答案】见解析
【解析】
(1)连接BE,根据线段垂直平分线的性质可得AE=BE,利用等边对等角的性质可得∠ABE=∠A;结合三角形外角的性质可得∠BEC的度数,再在Rt△BCE中结合含30°角的直角三角形的性质,即可证明第(1)问的结论;
(2)根据直角三角形斜边中线的性质可得BD=CD,再利用直角三角形锐角互余的性质可得到∠ABC=60°,至此不难判断△BCD的形状
(1)证明:连结BE,如图.
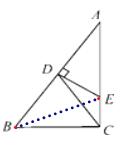
∵DE是AB的垂直平分线,
∴AE=BE,
∴∠ABE=∠A=30°,
∴∠CBE=∠ABC-∠ABE=30°,
在Rt△BCE中,BE=2CE,
∴AE=2CE.
(2)解:△BCD是等边三角形.
理由如下:
∵DE垂直平分AB,
∴D为AB的中点.
∵∠ACB=90°,
∴CD=BD.
又∵∠ABC=60°,
∴△BCD是等边三角形.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,已知:
中,已知:![]() ,
,![]() ,
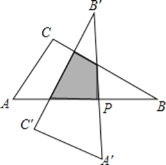
,![]() ,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转
,以斜边AB的中点P为旋转中心,把这个三角形按逆时针方向旋转![]() 得到
得到![]() ,则旋转前后两个直角三角形重叠部分的面积为______
,则旋转前后两个直角三角形重叠部分的面积为______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一食堂需要购买盒子存放食物,盒子有A、B两种型号,单个盒子的容量和价格如表格所示.现有15升食物需要存放且要求每个盒子都要装满,由于A型号盒子正做促销活动:购买三个及三个以上可一次性每个返还现金1.5元,则该食堂购买盒子所需的最少费用是 .
型号 | A | B |
单个盒子容量(升) | 2 | 3 |
单价(元) | 5 | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若十位上的数字比个位上的数字、百位上的数字都大的三位数叫做中高数,如796就是一个“中高数”.若一个三位数的十位上数字为7,且从4、5、6、8中随机选取两数,与7组成“中高数”,那么组成“中高数”的概率是多少?(请用“画树状图”或“列表”等方法写出分析过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线 ![]() (其中
(其中 ![]() )与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.
)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,抛物线的对称轴l与x轴交于点D,且点D恰好在线段BC的垂直平分线上.
(1)求抛物线的关系式;
(2)过点 ![]() 的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标.
的线段MN∥y轴,与BC交于点P,与抛物线交于点N.若点E是直线l上一点,且∠BED=∠MNB-∠ACO时,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距70千米,甲从A地出发,每小时行15千米,乙从B地出发,每小时行20千米.
(1)若两人同时出发,相向而行,则经过几小时两人相遇?
(2)若甲在前,乙在后,两人同时同向而行,则几小时后乙追上甲?
(3)若两人同时出发,相向而行,则几小时后两人相距10千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某检修小组乘汽车从![]() 地出发,在东西走向的马路上检修线路,如果规定向东行驶为正,一天中七个检修点的行驶记录如下(单位:
地出发,在东西走向的马路上检修线路,如果规定向东行驶为正,一天中七个检修点的行驶记录如下(单位:![]() ):
):
-4,+7,-9,+8,+6,-4,-3.
(1)收工时汽车共行驶了多少千米?
(2)收工时,汽车距![]() 地多远?
地多远?
(3)在检修时,第几个检修点离![]() 地最远,最远距离是多少?
地最远,最远距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在下列各图中,点O为直线AB上一点,∠AOC=60°,直角三角板的直角顶点放在点处.
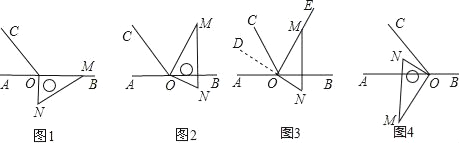
(1)如图1,三角板一边OM在射线OB上,另一边ON在直线AB的下方,则∠BOC的度数为 °,∠CON的度数为 °;
(2)如图2,三角板一边OM恰好在∠BOC的角平分线OE上,另一边ON在直线AB的下方,此时∠BON的度数为 °;
(3)请从下列(A),(B)两题中任选一题作答.
我选择: .
(A)在图2中,延长线段NO得到射线OD,如图3,则∠AOD的度数为 °;∠DOC与∠BON的数量关系是∠DOC ∠BON(填“>”、“=”或“<”);
(B)如图4,MN⊥AB,ON在∠AOC的内部,若另一边OM在直线AB的下方,则∠COM+∠AON的度数为 °;∠AOM﹣∠CON的度数为 °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将等腰△ABC绕顶点B逆时针方向旋转α度到△A1B1C1的位置,AB与A1C1相交于点D,AC与A1C1、BC1分别交于点E、F.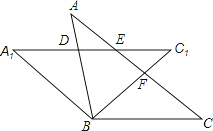
(1)求证:△BCF≌△BA1D.
(2)当∠C=α度时,判定四边形A1BCE的形状并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com