
【题目】如图:在△ABC中,BE,CF分别是AC,AB两边上的高,在BE上截取BD=AC,在CF的延长线上截取CG=AB,连接AD,AG. 
(1)求证:AD=AG;
(2)AD与AG的位置关系如何,请说明理由.
【答案】
(1)证明:∵BE⊥AC,CF⊥AB,
∴∠HFB=∠HEC=90°,又∵∠BHF=∠CHE,
∴∠ABD=∠ACG,
在△ABD和△GCA中
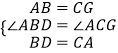 ,
,
∴△ABD≌△GCA(SAS),
∴AD=GA(全等三角形的对应边相等)
(2)位置关系是AD⊥GA,
理由为:∵△ABD≌△GCA,
∴∠ADB=∠GAC,
又∵∠ADB=∠AED+∠DAE,∠GAC=∠GAD+∠DAE,
∴∠AED=∠GAD=90°,
∴AD⊥GA.

【解析】(1)由BE垂直于AC,CF垂直于AB,利用垂直的定义得∠HFB=∠HEC,由得对顶角相等得∠BHF=∠CHE,所以∠ABD=∠ACG.再由AB=CG,BD=AC,利用SAS可得出三角形ABD与三角形ACG全等,由全等三角形的对应边相等可得出AD=AG,(2)利用全等得出∠ADB=∠GAC,再利用三角形的外角和定理得到∠ADB=∠AED+∠DAE,又∠GAC=∠GAD+∠DAE,利用等量代换可得出∠AED=∠GAD=90°,即AG与AD垂直.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】为了解食品安全状况,质监部门抽查了甲、乙、丙、丁四个品牌饮料的质量,将收集的数据整理并绘制成图1和图2两幅尚不完整的统计图,请根据图中的信息,完成下列问题:
(1)这次抽查了四个品牌的饮料共 瓶;
(2)请你在答题卡上补全两幅统计图;
(3)若四个品牌饮料的平均合格率是95%,四个品牌饮料月销售量约20万瓶,请你估计这四个品牌的不合格饮料有多少瓶?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图①所示放置,图②是由它抽象出的几何图形,B,C,E在同一条直线上,连接DC, 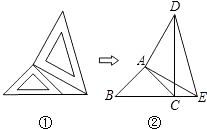
(1)请找出图②中的全等三角形,并给予说明(说明:结论中不得含有未标识的字母);
(2)试说明:DC⊥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学在一次用频率估计概率的实验中统计了某一结果出现的频率给出的统计图如图所示,则符合这一结果的实验可能是( )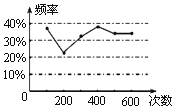
A.掷一枚正六面体的骰子,出现5点的概率
B.掷一枚硬币,出现正面朝上的概率
C.任意写出一个整数,能被2整除的概率
D.一个袋子中装着只有颜色不同,其他都相同的两个红球和一个黄球,从中任意取出一个是黄球的概率
查看答案和解析>>
科目:初中数学 来源: 题型:
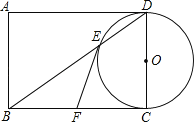
【题目】如图,以矩形ABCD的边CD为直径作⊙O,交矩形的对角线BD于点E,点F是BC的中点,连接EF.
(1)试判断EF与⊙O的位置关系,并说明理由.
(2)若DC=2,EF=![]() ,点P是⊙O上不与E、C重合的任意一点,则∠EPC的度数为 (直接写出答案)
,点P是⊙O上不与E、C重合的任意一点,则∠EPC的度数为 (直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正比例函数y=(a+1)x的图象经过第二四象限,若a同时满足方程x2+(1-2a)x+a2=0,判断此方程根的情况_________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张长方形纸条上画一条数轴. 
(1)若折叠纸条,数轴上表示﹣3的点与表示1的点重合,则折痕与数轴的交点表示的数为;
(2)若经过某次折叠后,该数轴上的两个数a和b表示的点恰好重合,则折痕与数轴的交点表示的数为(用含a,b的代数式表示);
(3)若将此纸条沿虚线处剪开,将中间的一段纸条对折,使其左右两端重合,这样连续对折n次后,再将其展开,请分别求出最左端的折痕和最右端的折痕与数轴的交点表示的数.(用含n的代数式表示)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com