
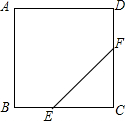
 如图,在边长为12cm的正方形ABCD中,点E从点B开始沿边BC以2cm/s的速度向点C移动,点F从点C开始沿边CD以2cm/s的速度向点D移动.
如图,在边长为12cm的正方形ABCD中,点E从点B开始沿边BC以2cm/s的速度向点C移动,点F从点C开始沿边CD以2cm/s的速度向点D移动.分析 (1)用含t的代数式表述出CE、CF,通过直角三角形CEF的面积把S与t连接起来.由于E、F只能在BC、CD上移动,可确定t的取值范围;
(2)把S=16代入函数关系式,解一元二次方程求出t的值;
(3)把S=20代入函数关系式,若方程有解,则有t满足△CEF的面积为20cm2,求出CE,反之△CEF的面积不能为20m2.
解答 解:(1)CE=BC-BE=12-2t,
∵0<CE<12,∴0<t<6
ts时,CE=BC-BE=12-2t,CF=2t,
在RT△CEF中,
∵△CEF=$\frac{1}{2}$CE×CF=$\frac{1}{2}$(12-2t)×2t=12t-2t2.
∴S=12t-2t2(0<t<6).
(2)当S=16时,12t-2t2=16,
即t2-6t+8=0,
解得:t1=2,t2=4.
当t为2s或4s时,△CEF的面积为16cm2.
(3)△CEF的面积不能为20m2.
把S=20代入函数关系式,得12t-2t2=20,
即t2-6t+10=0,
∵△=b2-4ac=(-6)2-4×1×10=-4<0,
∴原方程无实数根.
即没有t满足△CEF的面积能为20cm2.
点评 此题是个含动点类的题目,考察了直角三角形的面积、写二次函数表达式、22解一元二次方程及根的判别式.利用直角三角形的面积,把几何问题转化为函数关系,是解决本题的关键.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
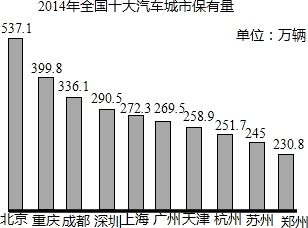 2014年国内汽车保有量将近1.4亿,就2013全国汽牢保有量已达到1.37亿辆,从2400万辆增长到1.37亿期,近十年汽车年均增加1100多万辆,是2003年汽车数量的5.7倍,全国有31个城市的汽车数量超过100万辆.
2014年国内汽车保有量将近1.4亿,就2013全国汽牢保有量已达到1.37亿辆,从2400万辆增长到1.37亿期,近十年汽车年均增加1100多万辆,是2003年汽车数量的5.7倍,全国有31个城市的汽车数量超过100万辆.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,抛物线y=ax(x-2)(0<a<4)与x轴交于O,A两点,顶点为M,对称轴交抛物线y=(4-a)x2于点B,连接OB,AB,OM,AM,四边形OMAB面积为s.
如图,在平面直角坐标系中,抛物线y=ax(x-2)(0<a<4)与x轴交于O,A两点,顶点为M,对称轴交抛物线y=(4-a)x2于点B,连接OB,AB,OM,AM,四边形OMAB面积为s.| a | 1 | 2 | 3 |
| s |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 考试分数(分) | 20 | 16 | 12 | 8 |
| 人数 | 24 | 18 | 5 | 3 |
| A. | 20,16 | B. | l6,20 | C. | 20,l2 | D. | 16,l2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
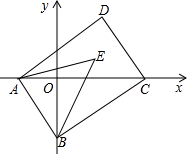 如图,在平面直角坐标系中,已知A(a,0),B(0,b)两点,且a、b满足(3a-2b)2+|a-b-1|=0,点C(m,0)在x轴的正半轴上,将线段AB平移到DC,连接对应点A、D和B、C,请回答下列问题:
如图,在平面直角坐标系中,已知A(a,0),B(0,b)两点,且a、b满足(3a-2b)2+|a-b-1|=0,点C(m,0)在x轴的正半轴上,将线段AB平移到DC,连接对应点A、D和B、C,请回答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com