【题目】已知：如图所示，AC=CD，∠B=∠E=90°，AC⊥CD，则不正确的结论是（ ）
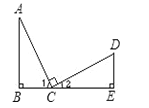
A. ∠1=∠2 B. ∠A =∠2 C. △ABC≌△CED D. ∠A与∠D互为余角
【答案】A
【解析】试题分析：A选项：因为AC⊥CD，∠ACD=90°，所以可得：∠1+∠2=90°，所以A选项错误；
B选项：因为AC⊥CD，∠ACD=90°，所以可得：∠1+∠2=90°，又因为∠B=90°，所以∠1+∠A=90°，根据同角的余角相等可得：∠A=∠2，故B选项正确；
C选项：因为AC⊥CD，∠ACD=90°，所以可得：∠1+∠2=90°，又因为∠B=90°，所以∠1+∠A=90°，根据同角的余角相等可得：∠A=∠2，又因为AC=CD,∠B=∠E，根据AAS可证△ABC≌△CED，故C选项正确；
D选项：因为AC⊥CD，∠ACD=90°，所以可得：∠1+∠2=90°，又因为∠B=90°，所以∠1+∠A=90°，根据同角的余角相等可得：∠A=∠2，因为∠E=90°，所以∠D+∠2=90°，所以∠A+∠D＝90°，所以∠A和∠D互为余角，故D选项正确.
故应选A.
科目：初中数学 来源： 题型：
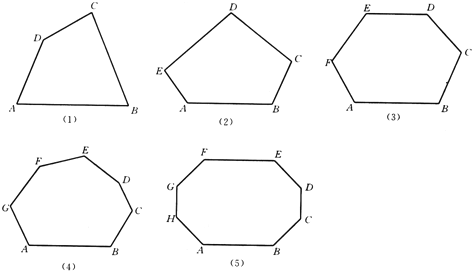
【题目】分别画出下列各多边形的对角线，并观察图形完成下列问题：
（1）试写出用n边形的边数n表示对角线总条数S的式子： ．
（2）从十五边形的一个顶点可以引出 条对角线，十五边形共有 条对角线：
（3）如果一个多边形对角线的条数与它的边数相等，求这个多边形的边数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图在Rt△ABC中，∠BAC=90 o，AC=2AB，点D是AC的中点,将一块锐角为45 o的直角三角板如图放置，使三角板斜边的两个端点分别与A，D重合，连接BE，EC。试猜想线段BE和EC的数量及位置关系，并证明你的猜想。
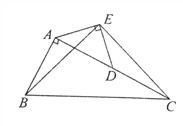
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为了测量校园水平地面上一棵树的高度，数学兴趣小组利用一根标杆、皮尺，设计如图所示的测量方案.已知测量同学眼睛A、标杆顶端F、树的顶端E在同一直线上，此同学眼睛距地面1.6米，标杆高为3.2米，且BC=2米，CD=6米，求树ED的高．
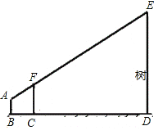
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，随机选取该校部分学生进行调查，要求每名学生从中只选一类最喜爱的电视节目.以下是根据调查结果绘制的统计图表的一部分.
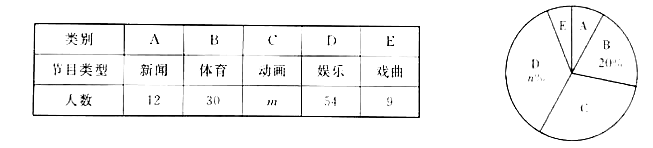
根据以上信息，解答下列问题：
（1）被调查的学生中，最喜爱体育节目的有 人，这些学生数占被调查总人数的百分比为 %；
（2）被调查学生的总数为 人，统计表中
的值为 ，统计图中
的值为 ；
（3）在统计图中，
类所对应扇形圆心角的度数为 ；
（4）该校共有2000名学生，根据调查结果，估计该校最喜爱欣慰节目的学生数.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下列材料：
问题：已知方程x2+x﹣1=0，求一个一元二次方程，使它的根分别是已知方程根的2倍．
解：设所求方程的根为y，则y=2x，所以x=
，把x=
，代入已知方程，
得（
）2 +
﹣1=0．
化简，得y2+2y﹣4=0，
故所求方程为y2+2y﹣4=0
这种利用方程根的代换求新方程的方法，我们称为“换根法”．
请用阅读材料提供的“换根法”求新方程（要求：把所求方程化为一般形式）：
（1）已知方程x2+2x﹣1=0，求一个一元二次方程，使它的根分别是已知方程根的相反数，则所求方程为 ；
（2）已知关于x的一元二次方程ax2+bx+c=0（a≠0）有两个不等于零的实数根，求一个一元二次方程，使它的根分别是已知方程根的倒数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com