练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知抛物线的解析式为，则下列说法中错误的是（ ）

    A.确定抛物线的开口方向与大小

    B.若将抛物线沿轴平移，则，的值不变

    C.若将抛物线沿轴平移，则的值不变

    D.若将抛物线沿直线：平移，则、、的值全变

    【答案】D

    【解析】

    利用二次函数的性质对A进行判断；利用二次函数图象平移的性质对B、C、D进行判断．

    解：A、确定抛物线的开口方向与大小，说法正确；

    B、若将抛物线C沿y轴平移，则抛物线的对称轴不变，开口大小、开口方向不变，即a，b的值不变，说法正确；

    C、若将抛物线C沿x轴平移，抛物线的开口大小、开口方向不变，即a的值不变，说法正确；

    D、若将抛物线C沿直线l：y＝x＋2平移，抛物线的开口大小、开口方向不变，即a不变，b、c的值改变，说法错误；

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

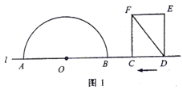
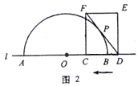
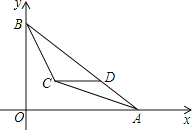
    【题目】如图1,点和矩形的边都在直线上,以点为圆心,以24为半径作半圆,分别交直线于两点.已知: ,,矩形自右向左在直线上平移,当点到达点时,矩形停止运动.在平移过程中,设矩形对角线与半圆的交点为 (点为半圆上远离点的交点).

    （1）如图2，若与半圆相切，求的值；

    （2）如图3，当与半圆有两个交点时，求线段的取值范围；

    （3）若线段的长为20，直接写出此时的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡，根据它们的质量（单位：），绘制出如下的统计图①和图②.请根据相关信息，解答下列问题：

    （Ⅰ）图①中的值为 ；

    （Ⅱ）求统计的这组数据的平均数、众数和中位数；

    （Ⅲ） 根据样本数据，估计这2500只鸡中，质量为的约有多少只？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

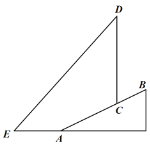
    【题目】为践行“绿水青山就是金山银山”的重要思想，某森林保护区开展了寻找古树活动．如图，在一个坡度（或坡比）i＝1:2.4的山坡AB上发现有一棵古树CD．测得古树底端C到山脚点A的距离AC＝26米，在距山脚点A水平距离6米的点E处，测得古树顶端D的仰角∠AED＝48°（古树CD与山坡AB的剖面、点E在同一平面上，古树CD与直线AE垂直），则古树CD的高度约为多少米？（参考数据：sin48°≈0.73，cos48°≈0.67，tan48°≈1.11）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，有四张背面相同的纸牌A、B、C、D，其正面分别画有四个不同的图形，小明将这四张纸牌背面朝上洗匀后随机摸出一张，放回后洗匀再随机摸出一张．

    （1）用树状图（或列表法）表示两次摸牌所有可能出现的结果（纸牌用A、B、C、D表示）；

    （2）求两次摸出的牌面图形既是中心对称图形又是轴对称图形的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

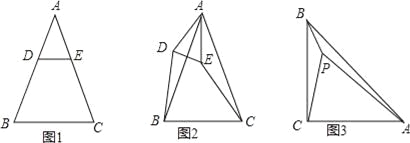
    【题目】已知△ABC是等腰三角形，AB=AC．

    （1）特殊情形：如图1，当DE∥BC时，有DB EC．（填“＞”，“＜”或“=”）

    （2）发现探究：若将图1中的△ADE绕点A顺时针旋转α（0°＜α＜180°）到图2位置，则（1）中的结论还成立吗？若成立，请给予证明；若不成立，请说明理由．

    （3）拓展运用：如图3，P是等腰直角三角形ABC内一点，∠ACB=90°，且PB=1，PC=2，PA=3，求∠BPC的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，平面直角坐标系中，A（8，0），B（0，6），∠BAO，∠ABO的平分线相交于点C，过点C作CD∥x轴交AB于点D，则点D的坐标为（　　）

    A.（ ，2）B.（ ，1）C.（ ，2）D.（，1）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将矩形纸片放在平面直角坐标系中,为坐标原点,点在轴上，点在轴上，点的坐标是，点是边上的-一个动点，将沿折叠，使点落在点处．

    如图①．当点恰好落在上时，求点的坐标；

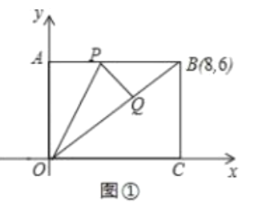
    (2)如图②，当点是中点时，直线交于点，

    求证：；

    求点的坐标．

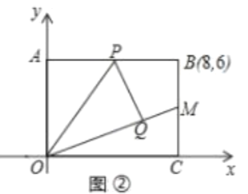
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知二次函数y＝（a﹣1）x2+3ax+1图象上的四个点的坐标为（x1，m），（x2，m），（x3，n），（x4，n），其中m＜n．下列结论可能正确的是（　　）

    A.若a＞，则 x1＜x2＜x3＜x4

    B.若a＞，则 x4＜x1＜x2＜x3

    C.若a＜﹣，则 x1＜x3＜x2＜x4

    D.若a＜﹣，则 x3＜x2＜x1＜x4

    查看答案和解析>>

    同步练习册答案