
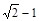 ,直线
,直线 与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M。
与坐标轴分别交于A、C两点,点B的坐标为(4,1),⊙B与x轴相切于点M。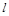 绕点A顺时针匀速旋转,当⊙B第一次与⊙O相切时,直线
绕点A顺时针匀速旋转,当⊙B第一次与⊙O相切时,直线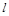 也恰好与⊙B第一次相切,见图(2)求B1的坐标以及直线AC绕点A每秒旋转多少度?
也恰好与⊙B第一次相切,见图(2)求B1的坐标以及直线AC绕点A每秒旋转多少度?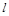 不动,⊙B沿x轴负方向平移过程中,能否与⊙O与直线
不动,⊙B沿x轴负方向平移过程中,能否与⊙O与直线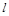 同时相切。若相切,说明理由。
同时相切。若相切,说明理由。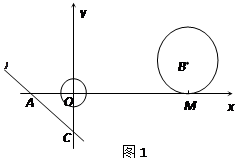
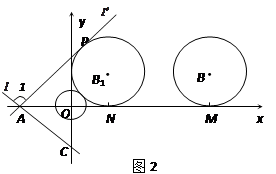
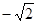 ,0)
,0)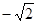 ). ∴ OA=OC ∵ OA⊥OC, ∴∠CAO=45°
). ∴ OA=OC ∵ OA⊥OC, ∴∠CAO=45° 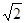 , B1N=1,B1N⊥AN.
, B1N=1,B1N⊥AN.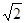 ,∴∠A B1O="∠NA" B1. ∴∠PA B1=∠A B1O. ∴PA∥B1O.
,∴∠A B1O="∠NA" B1. ∴∠PA B1=∠A B1O. ∴PA∥B1O.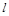 同时相切。
同时相切。

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:解答题
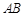 是⊙
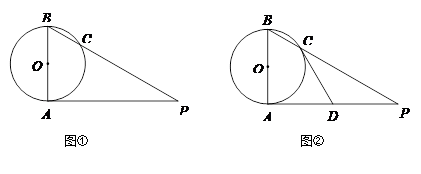
是⊙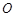 的直径,
的直径,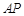 是⊙
是⊙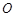 的切线,
的切线,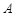 是切点,
是切点, 与⊙
与⊙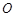 交于点
交于点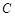 .
.
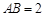 ,
,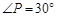 ,求
,求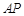 的长(结果保留根号);
的长(结果保留根号);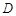 为
为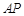 的中点,求证:直线
的中点,求证:直线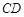 是⊙
是⊙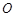 的切线.
的切线.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
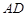 为
为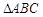 外接圆的直径,
外接圆的直径,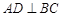 ,垂足为点
,垂足为点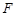 ,
,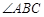 的平分线交
的平分线交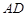 于点
于点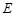 ,连接
,连接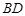 ,
,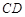 。
。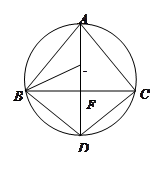
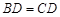 ;
; 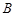 ,
,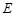 ,
,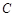 三点是否在以
三点是否在以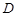 为圆心,以
为圆心,以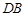 为半径的圆上?并说明理由。
为半径的圆上?并说明理由。查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
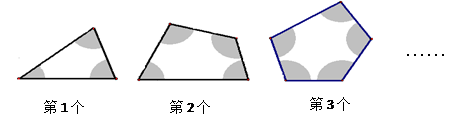
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
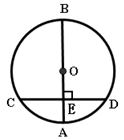
| A.点E在小⊙O外 | B.点E在小⊙O上 | C.点E在小⊙O内 | D.不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com