
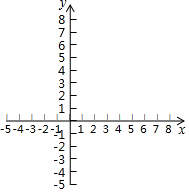 数学李老师给学生出了这样一个问题:探究函数y=$\frac{x}{x+1}$的图象与性质,小斌根据学习函数的经验,对函数y=$\frac{x}{x+1}$的图象与性质进行了探究.下面是小斌的探究过程,请您补充完成:
数学李老师给学生出了这样一个问题:探究函数y=$\frac{x}{x+1}$的图象与性质,小斌根据学习函数的经验,对函数y=$\frac{x}{x+1}$的图象与性质进行了探究.下面是小斌的探究过程,请您补充完成:| x | … | -5 | -4 | -3 | -2 | -$\frac{3}{2}$ | -$\frac{1}{2}$ | 0 | 1 | 2 | m | 4 | 5 | … |
| y | … | $\frac{5}{4}$ | $\frac{4}{3}$ | $\frac{3}{2}$ | 2 | 3 | -1 | 0 | $\frac{1}{2}$ | $\frac{2}{3}$ | $\frac{3}{4}$ | $\frac{4}{5}$ | $\frac{5}{6}$ | … |
分析 (1)根据分母非零即可得出x+1≠0,解之即可得出自变量x的取值范围;
(2)将y=$\frac{3}{4}$代入函数解析式中求出x值即可;
(3)描点、连线画出函数图象;
(4)观察函数图象,写出函数的一条性质即可.
解答 解:(1)∵x+1≠0,
∴x≠-1.
故答案为:x≠-1.
(2)当y=$\frac{x}{x+1}$=$\frac{3}{4}$时,x=3.
故答案为:3.
(3)描点、连线画出图象如图所示.
(4)观察函数图象,发现:函数y=$\frac{x}{x+1}$在x<-1和x>-1上均单调递增.
点评 本题考查了反比例函数的性质以及函数图象,根据给定数据描点、连线画出函数图象是解题的关键.


 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3a+6b+9c)元 | B. | (9a+6b+3c)元 | C. | 6(a+b+c)元 | D. | (3+6+9)(a+b+c)元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙M与菱形ABCD在平面直角坐标系中,点M的坐标为(3,-1),点A的坐标为(-2,$\sqrt{3}$),点B的坐标为(-3,0),点C在x轴上,且点D在点A的左侧.
如图,⊙M与菱形ABCD在平面直角坐标系中,点M的坐标为(3,-1),点A的坐标为(-2,$\sqrt{3}$),点B的坐标为(-3,0),点C在x轴上,且点D在点A的左侧.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com