
【题目】已知∠MAN=135°,正方形ABCD绕点A旋转.
(1)当正方形ABCD旋转到∠MAN的外部(顶点A除外)时,AM,AN分别与正方形ABCD的边CB,CD的延长线交于点M,N,连接MN.
①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是 ;
②如图2,若BM≠DN,请判断①中的数量关系是否仍成立?若成立,请给予证明;若不成立,请说明理由;
(2)如图3,当正方形ABCD旋转到∠MAN的内部(顶点A除外)时,AM,AN分别与直线BD交于点M,N,探究:以线段BM,MN,DN的长度为三边长的三角形是何种三角形,并说明理由.

【答案】(1)①MN=BM+DN;②成立;(2)直角三角形.
【解析】
试题分析:(1)①如图1,先证明△ADN≌△ABM,得到AN=AM,∠NAD=∠MAB,得到∠NAD=∠MAB=67.5°.作AE⊥MN于E,由等腰三角形三线合一的性质得出MN=2NE,∠NAE=67.5°.再证明△ADN≌△AEN,得出DN=EN,进而得到MN=BM+DN;
②如图2,先证明△ABM≌△ADP,得出AM=AP,∠1=∠2=∠3,再计算出∠PAN=135°.然后证明△ANM≌△ANP,得到MN=PN,进而得到MN=BM+DN;
(2)如图3,将△ABM绕点A逆时针旋转90°,得到△ADE,连结NE.由旋转的性质得到DE=BM,AE=AM,∠EAM=90°,∠NDE=90°. 先证明△AMN≌△AEN.得到MN=EN.由DN,DE,NE为直角三角形的三边,得到以线段BM,MN,DN的长度为三边长的三角形是直角三角形.
试题解析:(1)①如图1,若BM=DN,则线段MN与BM+DN之间的数量关系是MN=BM+DN.理由如下:
在△ADN与△ABM中,∵AD=AB,∠ADN=∠ABM,DN=BM,∴△ADN≌△ABM(SAS),∴AN=AM,∠NAD=∠MAB,∵∠MAN=135°,∠BAD=90°,∴∠NAD=∠MAB=![]() (360°﹣135°﹣90°)=67.5°,作AE⊥MN于E,则MN=2NE,∠NAE=
(360°﹣135°﹣90°)=67.5°,作AE⊥MN于E,则MN=2NE,∠NAE=![]() ∠MAN=67.5°.在△ADN与△AEN中,∵∠ADN=∠AEN,∠NAD=∠NAE,AN=AN,∴△ADN≌△AEN(AAS),∴DN=EN,∵BM=DN,MN=2EN,∴MN=BM+DN.故答案为:MN=BM+DN;
∠MAN=67.5°.在△ADN与△AEN中,∵∠ADN=∠AEN,∠NAD=∠NAE,AN=AN,∴△ADN≌△AEN(AAS),∴DN=EN,∵BM=DN,MN=2EN,∴MN=BM+DN.故答案为:MN=BM+DN;
②如图2,若BM≠DN,①中的数量关系仍成立.理由如下:
延长NC到点P,使DP=BM,连结AP.∵四边形ABCD是正方形,∴AB=AD,∠ABM=∠ADC=90°.在△ABM与△ADP中,∵AB=AD,∠ABM=∠ADP,BM=DP,∴△ABM≌△ADP(SAS),∴AM=AP,∠1=∠2=∠3,∵∠1+∠4=90°,∴∠3+∠4=90°,∵∠MAN=135°,∴∠PAN=360°﹣∠MAN﹣(∠3+∠4)=360°﹣135°﹣90°=135°.在△ANM与△ANP中,∵AM=AP,∠MAN=∠PAN,AN=AN,∴△ANM≌△ANP(SAS),∴MN=PN,∵PN=DP+DN=BM+DN,∴MN=BM+DN;
(2)以线段BM,MN,DN的长度为三边长的三角形是直角三角形.理由如下:
如图3,将△ABM绕点A逆时针旋转90°,得到△ADE,连结NE.由旋转的性质得:DE=BM,AE=AM,∠EAM=90°,∠NDE=90°. ∵∠MAN![]() 135°,∴∠EAN
135°,∴∠EAN![]() 360°
360°![]() ∠MAN
∠MAN![]() ∠EAM =135°,∴∠EAN =∠MAN.在△AMN与△AEN中,∵AM=AE,∠MAN=∠EAN,AN=AN,∴△AMN≌△AEN.∴MN=EN.∵DN,DE,NE为直角三角形的三边,∴以线段BM,MN,DN的长度为三边长的三角形是直角三角形.
∠EAM =135°,∴∠EAN =∠MAN.在△AMN与△AEN中,∵AM=AE,∠MAN=∠EAN,AN=AN,∴△AMN≌△AEN.∴MN=EN.∵DN,DE,NE为直角三角形的三边,∴以线段BM,MN,DN的长度为三边长的三角形是直角三角形.




 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知线段AB=10cm,点C是直线AB上一点,BC=4cm,若M是AC的中点, N是BC的中点,则线段MN的长度是:( )
A.7cm
B.5cm或3cm
C.7cm或3cm
D.5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
“共享单车”是指企业与政府合作,在校园、地铁站点、公交站点、居民区、商业区、公共服务区等提供自行车共享的一种服务,是共享经济的一种新形态.共享单车的出现让更多的用户有了更好的代步选择.自行车也代替了一部分公共交通甚至打车的出行.
Quest Mobile监测的M型与O型单车从2016年10月——2017年1月的月度用户使用情况如下表所示:
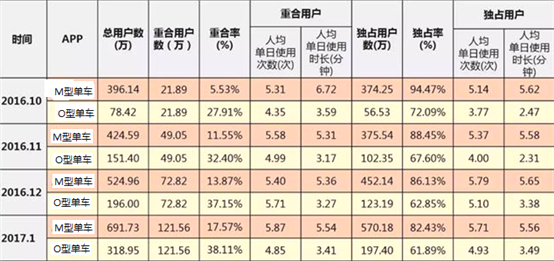
根据以上材料解答下列问题:
(1)仔细阅读上表,将O型单车总用户数用折线图表示出来,并在图中标明相应数据;
(2)根据图表所提提供的数据,选择你所感兴趣的方面,写出一条你发现的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥DE,AB=DE,BF=EC.
(1)求证:AC∥DF;
(2)若CF=1个单位长度,能由△ABC经过图形变换得到△DEF吗?若能,请你用轴对称、平移或旋转等描述你的图形变换过程;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA、OB分别是线段MC、MD的垂直平分线,MD=5cm,MC=7cm,CD=10cm,一只小蚂蚁从点M出发爬到OA边上任意一点E,再爬到OB边上任意一点F,然后爬回M点处,则小蚂蚁爬行的路径最短可为( ) 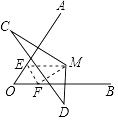
A.12cm
B.10cm
C.7cm
D.5cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l1:y=﹣x+3与直线l2:y=x+1相交于点A.并且l1交x轴于点B,l2交x轴于点C.若平面上有一点D,构成平行四边形ABDC,请写出D点坐标 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2015次运动后,动点P的坐标是( )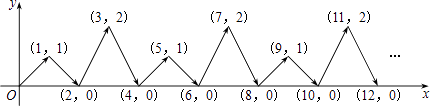
A.(2015,0)
B.(2015,1)
C.(2015,2)
D.(2016,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com