
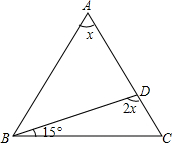
 如图,在△ABC中,∠ABC=∠ACB,求∠ADB度数.
如图,在△ABC中,∠ABC=∠ACB,求∠ADB度数. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
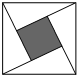 “赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形.学习《探索勾股定理》后,几位同学在上课用的道具上玩掷骰子的游戏,看谁能把骰子投到中间的小正方形中.若设直角三角形的两条直角边的长分别是1和2.你能算出骰子投在在中间小正方形区域(含边线)的概率吗?是$\frac{1}{5}$.
“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形.学习《探索勾股定理》后,几位同学在上课用的道具上玩掷骰子的游戏,看谁能把骰子投到中间的小正方形中.若设直角三角形的两条直角边的长分别是1和2.你能算出骰子投在在中间小正方形区域(含边线)的概率吗?是$\frac{1}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
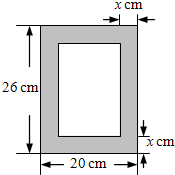 如图,某矩形相框长26cm,宽20cm,其四周相框边(图中阴影部分)的宽度相同,都是xcm,相框内部的面积(指图中较小矩形的面积)为ycm2,求y关于x的函数表达式,并写出自变量的取值范围.
如图,某矩形相框长26cm,宽20cm,其四周相框边(图中阴影部分)的宽度相同,都是xcm,相框内部的面积(指图中较小矩形的面积)为ycm2,求y关于x的函数表达式,并写出自变量的取值范围.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
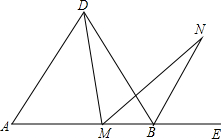 已知点M是等边△ABD中边AB上任意一点(不与A、B重合),作∠DMN=60°,交∠DBA外角平分线于点N.
已知点M是等边△ABD中边AB上任意一点(不与A、B重合),作∠DMN=60°,交∠DBA外角平分线于点N.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com