
分析 (1)先把二次根式化为最简二次根式,然后合并即可;
(2)先把二次根式化为最简二次根式,然后把括号内合并后进行二次根式的除法运算.
解答 解:(1)原式=2$\sqrt{2}$-2$\sqrt{2}$
=0;
(2)原式=(6$\sqrt{3}$-$\frac{2\sqrt{3}}{3}$+4$\sqrt{3}$)$÷2\sqrt{3}$
=$\frac{28\sqrt{3}}{3}$÷2$\sqrt{3}$
=$\frac{14}{3}$.
点评 本题考查了二次根式的混合运算:先把二次根式化为最简二次根式,然后进行二次根式的乘除运算,再合并即可.在二次根式的混合运算中,如能结合题目特点,灵活运用二次根式的性质,选择恰当的解题途径,往往能事半功倍.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
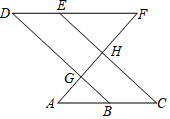 如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.
如图,点B、E分别在直线AC和DF上,若∠AGB=∠EHF,∠C=∠D,可以证明∠A=∠F.请完成下面证明过程中的各项“填空”.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 由5x+7=0,得5x=-7 | B. | 由2x-3=0,得2x-3+3=0 | ||
| C. | 由$\frac{x}{4}$=2,得x=$\frac{1}{2}$ | D. | 由3x=5,得x=15 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
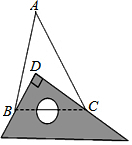 如图,已知在△ABC中,∠A=40°,将一块直角三角板放在△ABC上使三角板的两条直角边分别经过B、C,直角顶点D落在△ABC的内部,那么∠ABD+∠ACD=50度.
如图,已知在△ABC中,∠A=40°,将一块直角三角板放在△ABC上使三角板的两条直角边分别经过B、C,直角顶点D落在△ABC的内部,那么∠ABD+∠ACD=50度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com