
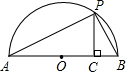
 已知a、b是正实数,那么,$\frac{a+b}{2}$$≥\sqrt{ab}$是恒成立的.
已知a、b是正实数,那么,$\frac{a+b}{2}$$≥\sqrt{ab}$是恒成立的.分析 (1)已知不等式左边利用完全平方公式化简,整理即可得证;
(2)连接OP,利用直径所对的圆周角为直角且PC与AB垂直,得到三角形APC与三角形PBC相似,由相似得比例表示出PC,根据垂线段最短即可得证.
解答 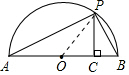 解:(1)由($\sqrt{a}-\sqrt{b}$)2≥0,得到a-2$\sqrt{ab}$+b≥0,
解:(1)由($\sqrt{a}-\sqrt{b}$)2≥0,得到a-2$\sqrt{ab}$+b≥0,
于是a+b≥2$\sqrt{ab}$,
则$\frac{a+b}{2}$≥$\sqrt{ab}$;
(2)连接OP,
∵AB为直径,
∴∠APB=90°,
∵PC⊥AB,
∴Rt△APC∽Rt△PBC,
∴$\frac{PC}{AC}$=$\frac{CB}{PC}$,即PC2=AC•CB=ab,
∴PC=$\sqrt{ab}$,
∵PO=$\frac{a+b}{2}$,
由垂线段最短得到PO≥PC,
则$\frac{a+b}{2}$≥$\sqrt{ab}$.
点评 此题考查了相似三角形的判定与性质,圆周角定理,以及垂径定理,熟练掌握相似三角形的判定与性质是解本题的关键.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:填空题
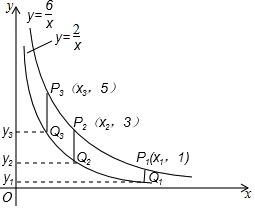 两个反比例函数y=$\frac{2}{x}$,y=$\frac{6}{x}$在第一象限内的图象如图所示,点P1,P2,P3…,P2017在反比例函数y=$\frac{6}{x}$图象上,它们的横坐标分别是x1,x2,x3…,x2017,纵坐标分别是1,3,5,…,共2017个连续奇数,过点P1,P2,P3,…P2017分别作y轴的平行线,与y=$\frac{2}{x}$的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…,Q2017(x2017,y2017),则y2017=$\frac{4033}{3}$.
两个反比例函数y=$\frac{2}{x}$,y=$\frac{6}{x}$在第一象限内的图象如图所示,点P1,P2,P3…,P2017在反比例函数y=$\frac{6}{x}$图象上,它们的横坐标分别是x1,x2,x3…,x2017,纵坐标分别是1,3,5,…,共2017个连续奇数,过点P1,P2,P3,…P2017分别作y轴的平行线,与y=$\frac{2}{x}$的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…,Q2017(x2017,y2017),则y2017=$\frac{4033}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20元 | B. | 19元 | C. | 18元 | D. | 17元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
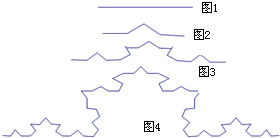 若图1中的线段长为1,将此线段三等分,并以中间的一段为边作等边三角形,然后去掉这一段,得到图2称第1次操作,再将图2中的每一段类似变形,得到图3即第2次操作,按上述方法继续得到图4为第3次操作,则第4次操作后折线的总长度为$\frac{64}{27}$.
若图1中的线段长为1,将此线段三等分,并以中间的一段为边作等边三角形,然后去掉这一段,得到图2称第1次操作,再将图2中的每一段类似变形,得到图3即第2次操作,按上述方法继续得到图4为第3次操作,则第4次操作后折线的总长度为$\frac{64}{27}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com