(1)证明:∵四边形ABCD是正方形,∴∠ABE=∠BCF=90°,AB=BC。∴∠ABF+∠CBF=90°。
∵AE⊥BF,∴∠ABF+∠BAE=90°。∴∠BAE=∠CBF。
在△ABE和△BCF中,∵∠ABE=∠BCF,AB=BC,∠BAE=∠CBF,
∴△ABE≌△BCF(ASA)。
(2)解:∵正方形面积为3,∴AB=

。
在△BGE与△ABE中,∵∠GBE=∠BAE,∠EGB=∠EBA=90°,∴△BGE∽△ABE。
∴

。
又∵BE=1,∴AE
2=AB
2+BE
2=3+1=4。
∴

。
(3)解:没有变化。理由如下:
∵AB=

,BE=1,∴

。∴∠BAE=30°。
∵AB′=AD,∠AB′E′=∠ADE'=90°,AE′= AE′,∴Rt△ABE≌Rt△AB′E′≌Rt△ADE′,
∴∠DAE′=∠B′AE′=∠BAE=30°。
∴AB′与AE在同一直线上,即BF与AB′的交点是G。
设BF与AE′的交点为H,
则∠BAG=∠HAG=30°,而∠AGB=∠AGH=90°,AG= AG,∴△BAG≌△HAG。
∴

。
∴△ABE在旋转前后与△BCF重叠部分的面积没有变化。
(1)由四边形ABCD是正方形,可得∠ABE=∠BCF=90°,AB=BC,又由AE⊥BF,由同角的余角相等,即可证得∠BAE=∠CBF,然后利用ASA,即可判定:△ABE≌△BCF。
(2)由正方形ABCD的面积等于3,即可求得此正方形的边长,由在△BGE与△ABE中,∠GBE=∠BAE,∠EGB=∠EBA=90°,可证得△BGE∽△ABE,由相似三角形的面积比等于相似比的平方,即可求得答案。
(3)由正切函数,求得∠BAE=30°,易证得Rt△ABE≌Rt△AB′E′≌Rt△ADE′,可得AB′与AE在同一直线上,即BF与AB′的交点是G,然后设BF与AE′的交点为H,可证得△BAG≌△HAG,从而证得结论


 (3)没有变化,理由见解析
(3)没有变化,理由见解析 。
。 。
。 。
。 ,BE=1,∴
,BE=1,∴ 。∴∠BAE=30°。
。∴∠BAE=30°。 。
。 

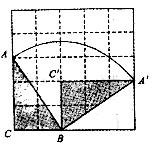
 ,∠ACB=90°,∠A=30°.若Rt△ABC由现在的位置向右滑动地旋转,当点A第3次落在直线l上时,点A所经过的路线的长为
,∠ACB=90°,∠A=30°.若Rt△ABC由现在的位置向右滑动地旋转,当点A第3次落在直线l上时,点A所经过的路线的长为
 ).
).




 时,求CM的长.
时,求CM的长.