
 如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC边于点D,交AC边于点G,过D作⊙O的切线EF,交AB的延长线于点F,交AC于点E.
如图,在△ABC中,AB=AC,以AB为直径作⊙O,交BC边于点D,交AC边于点G,过D作⊙O的切线EF,交AB的延长线于点F,交AC于点E.分析 (1)根据圆周角定理得出∠ADB=90°,再由等腰三角形的三线合一性质即可得出结论.
(2)推出△FOD∽△FAE,得出比例式,即可求出半径.
(3)求出∠F=30°,求出∠BOD=60°,得出等边三角形OBD,推出∠ABC=60°,根据等边三角形判定推出即可.
解答 (1)证明:连接AD,如图所示: ∵AB为直径,
∵AB为直径,
∴∠ADB=90°,
∵AB=AC,
∴BD=CD;
(2)解:设⊙O的半径是R,则FO=4+R,FA=4+2R,OD=R,
连接OD,如图所示:
∵AB=AC,
∴∠ABC=∠C,
∵OB=OD,
∴∠ABC=∠ODB,
∴∠ODB=∠C,
∴OD∥AC,
∴△FOD∽△FAE,
∴$\frac{OD}{AE}=\frac{FO}{FA}$,
∴$\frac{R}{6}=\frac{4+R}{4+2R}$,
即R2-R-12=0,
∵R为半径,
∴R=4,R=-3(舍去),
即⊙O的半径是4.
(3)△ABC是等边三角形;理由:
∵EF是⊙O的切线,
∴OD⊥EF,
∴∠ODF=90°,
∵FO=4+4=8,OD=4,
∴∠F=30°,
∴∠FOD=60°,
∵OB=OD,
∴△OBD是等边三角形,
∴∠ABC=60°,
∵AC=AB,
∴△ABC是等边三角形.
点评 本题是圆的综合题目,考查了相似三角形的性质和判定、切线的性质、等边三角形的性质和判定、圆周角定理、平行线性质、等腰三角形性质的应用等知识;本题难度较大,综合性强,特别是(2)中需要通过作辅助线证明三角形相似才能得出结果.


科目:初中数学 来源: 题型:选择题
| A. | 在367人中至少有两个人的生日相同 | |
| B. | 一次摸奖活动的中奖率是1%,那么摸100次必然会中一次奖 | |
| C. | 一副扑克牌中,随意抽取一张是红桃K,这是必然事件 | |
| D. | 一个不透明的袋中装有3个红球,5个白球,搅匀后想中任意摸出一个球,摸到红球的可能性大于摸到白球的可能性 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,直线AB:y=2x+2交x轴、y轴于B、A两点,交双曲线y=$\frac{k}{x}$于C、D点,若3S△ACD=2S△ADO,求k的值.
如图,直线AB:y=2x+2交x轴、y轴于B、A两点,交双曲线y=$\frac{k}{x}$于C、D点,若3S△ACD=2S△ADO,求k的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
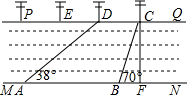 如图,河流的两岸MN、PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C、D、E…某人在河岸MN的A处测得∠DAN=38°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CF(结果精确到0.1,参考数据sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,Sin70°≈0.94,cos70°≈0.34,tan70°≈2.75).
如图,河流的两岸MN、PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C、D、E…某人在河岸MN的A处测得∠DAN=38°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CF(结果精确到0.1,参考数据sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,Sin70°≈0.94,cos70°≈0.34,tan70°≈2.75).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 个体 | B. | 总体 | C. | 总体的一个样本 | D. | 样本容量 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 干家务活平均时间 | 频数 | 百分比 |
| A | 10 | 25% |
| B | a | 62.5% |
| C | 5 | b |
| 合计 | c | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com