
����Ŀ����������ABCD�У�����BD��
��1����ͼ1��AE��BD��E��ֱ��д����BAE�Ķ�����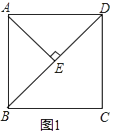
��2����ͼ1���ڣ�1���������£�����AEB��A��ת���ģ�����ʱ�뷽����ת30���õ���AB��E�䣬AB����BD����M��AE����ӳ�����BD����N��
�������ⲹȫͼ1��
���õ�ʽ��ʾ�߶�BM��DN��MN֮���������ϵ����֤����
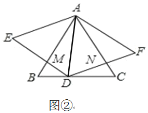
��3����ͼ2��E��F�DZ�BC��CD�ϵĵ㣬��CEF�ܳ���������ABCD�ܳ���һ�룬AE��AF�ֱ���BD����M��N��д���ж��߶�BM��DN��MN֮��������ϵ��˼·��������д�������������̣�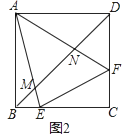
���𰸡�
��1���⣺��BD��������ABCD�ĶԽ��ߣ�
���ABD=��ADB=45�㣬
��AE��BD��
���ABE=��BAE=45�㣬
��2���⣺�������ⲹȫͼ�Σ���ͼ1��ʾ��
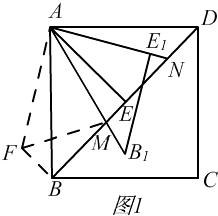
��BM��DN��MN֮���������ϵ��BM2+MD2=MN2��
����AND�Ƶ�D˳ʱ����ת90�㣬�õ���AFB��
���ADB=��FBA����BAF=��DAN��DN=BF��AF=AN��
����������ABCD��AE��BD��
���ADB=��ABD=45�㣬
���FBM=��FBA+��ABD=��ADB+��ABD=90�㣬
��Rt��BFM�У����ݹ��ɶ����ã�FB2+BM2=FM2��
����ת��ANE�õ�AB1E1��
���E1AB1=45�㣬
���BAB1+��DAN=90�㩁45��=45�㣬
�ߡ�BAF=DAN��
���BAB1+��BAF=45�㣬
���FAM=45�㣬
���FAM=��E1AB1��
��AM=AM��AF=AN��
���AFM�ա�ANM��
��FM=MN��
��FB2+BM2=FM2��
��DN2+BM2=MN2��
��3���⣺��ͼ2��
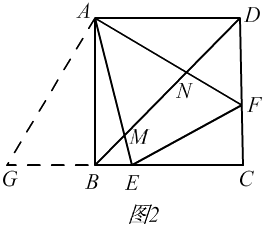
����ADF�Ƶ�A˳ʱ����ת90��õ���ABG��
��DF=GB��
��������ABCD���ܳ�Ϊ4AB��
��CEF�ܳ�ΪEF+EC+CF��
�ߡ�CEF�ܳ���������ABCD�ܳ���һ�룬
��4AB=2��EF+EC+CF����
��2AB=EF+EC+CF
��EC=AB��BE��CF=AB��DF��
��2AB=EF+AB��BE+AB��DF��
��EF=DF+BE��
��DF=GB��
��EF=GB+BE=GE��
����ת�õ�AD=AG=AB��
��AM=AM��
���AEG�ա�AEF��
��EAG=��EAF=45�㣬
�ͣ�2���Ģ�һ�����õ�DN2+BM2=MN2��
����������1���������������ʺ͵���ֱ�����������ʿ��������2��ͨ����ת����ȫ�������Σ�����ANDȫ���ڡ�AFB�� ������FBM=��FBA+��ABD=��ADB+��ABD=90�㣬�õ���AFM�ա�ANM��ת��FM=MN�������ó�����֮��Ĺ��ɹ�ϵ; ��3�������2����˼·�������Կɲ�����ת��������ȫ�������Ρ�ADF��ABG����һ����AEG�ա�AEF���ó�����֮��Ĺ�ϵ.
�����㾫�������ڱ��⿼��Ĺ��ɶ����ĸ����Ҫ�˽�ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2���ܵó���ȷ�𰸣�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OABC�Ķ���A��C�ֱ���![]() ���������ϣ���B������Ϊ(3,4)һ�κ���
���������ϣ���B������Ϊ(3,4)һ�κ���![]() ��ͼ�����OC��AB�ֱ��ڵ�D��E����������OD= BE.��M���߶�DE�ϵ�һ������.
��ͼ�����OC��AB�ֱ��ڵ�D��E����������OD= BE.��M���߶�DE�ϵ�һ������.
(1)��b��ֵ��
(2)����OM����������ODM��������ı���OAEM�����֮��Ϊ1��3�����M�����ꣻ
(3)���N��![]() ���Ϸ�ƽ���ڵ�һ�㣬��O��D��M��NΪ������ı��������Σ����N������.
���Ϸ�ƽ���ڵ�һ�㣬��O��D��M��NΪ������ı��������Σ����N������.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪MB=ND����MBA=��NDC�������ĸ����������ж���ABM�ա�CDN�� ��

A.AM=CNB.AB=CD C.AM��CN D.��M=��N
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���֪A��B��������y=ax2��a��0����������ͬ�ĵ㣬����A�ڵڶ����ޣ�B�ڵ�һ���ޣ�
��1����ͼ1��ʾ����ֱ��AB��x��ƽ�У���AOB=90�㣬��AB=2ʱ����������ߵĽ���ʽ��A��B����ĺ�����ij˻���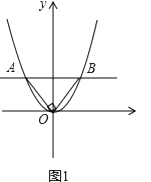
��2����ͼ2��ʾ���ڣ�1������õ��������ϣ���ֱ��AB��x�ƽ�У���AOB��Ϊ90��ʱ����֤��A��B���������ij˻���һ����ֵ��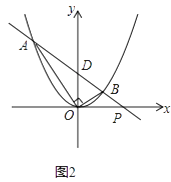
��3���ڣ�2���������£����ֱ��AB��x�ᡢy��ֱ��ڵ�P��D���ҵ�B�ĺ�����Ϊ ![]() ����ô��x�����Ƿ����һ��Q��ʹ��QDPΪ���������Σ������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
����ô��x�����Ƿ����һ��Q��ʹ��QDPΪ���������Σ������ڣ���ֱ��д����Q�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
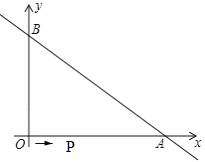
����Ŀ����ͼ��ֱ��![]() ��������ֱ���A��B���㣬OA=8��OB=6������P��O���������·��O��A��B��ÿ��2����λ���ȵ��ٶ��˶�������B��ʱ�˶�ֹͣ��
��������ֱ���A��B���㣬OA=8��OB=6������P��O���������·��O��A��B��ÿ��2����λ���ȵ��ٶ��˶�������B��ʱ�˶�ֹͣ��
(1)��A�������Ϊ_____��B���������Ϊ______��
(2)����P��OA�ϣ���BPƽ�֡�OBAʱ�����ʱ��P������Ϊ______��
(3)���P���˶�ʱ��Ϊt��(0��t��4)����BPA�����ΪS����S��t֮��ĺ�����ϵʽ����ֱ��д����S=8ʱ��P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���Ϳ�����Ⱦ�������ɺ�����˾����ȫ���������ܻ�����ȼ�����������ƻ�����A�ͺ�B�����ֹ�������10��������ÿ̨�ļ۸����ؿ��������
A�� | B�� | |
�۸���Ԫ/̨�� | a | b |
���ؿ���������/�꣩ | 60 | 100 |
������A������1����B������2��������400��Ԫ��������A������2����B������1��������350��Ԫ��
��1����a��b��ֵ��
��2������ù�˾����A�ͺ�B���������ܷ��ò�����1200��Ԫ����ȷ����10���������ڸ���·������ؿ��ܺͲ�����680���˴Σ��������һ��������ʹ�ù����ܷ������٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����⣺���ǰѶԷǸ�ʵ��![]() ����������������λ��ֵ��Ϊ
����������������λ��ֵ��Ϊ![]() ��
��
����![]() Ϊ�Ǹ�����ʱ����
Ϊ�Ǹ�����ʱ����![]() ����
����![]() ��
��
���磺![]() ��
��![]() ������
������
�����������⣺
��1��![]() ______��
______��
��2����![]() ����ʵ��
����ʵ��![]() ��ȡֵ��Χ��_________��
��ȡֵ��Χ��_________��
��3����![]() ��
��
�ڵ�![]() Ϊ�Ǹ�����ʱ��
Ϊ�Ǹ�����ʱ��![]() ��
��
������![]() �ķǸ�ʵ��
�ķǸ�ʵ��![]() ֻ�����������н�����ȷ����_____������ţ�
ֻ�����������н�����ȷ����_____������ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ijͬѧ�Զ���ʽ��x2��4x+2����x2��4x+6��+4������ʽ�ֽ�Ĺ��̣�
�⣺��x2��4x=y
ԭʽ=��y+2����y+6��+4 ����һ����
=y2+8y+16 ���ڶ�����
=��y+4��2����������
=��x2��4x+4��2�����IJ���
�ش��������⣺
��1����ͬѧ�ڶ�������������������ʽ�ֽ��_______��
A����ȡ����ʽ |
B��ƽ���ʽ |
C�������͵���ȫƽ����ʽ |
D�����������ȫƽ����ʽ |
��2����ͬѧ��ʽ�ֽ�Ľ���Ƿף�________�����������������������������������ף���ֱ��д����ʽ�ֽ�������_________ ��
��3������ģ�����Ϸ������ԶԶ���ʽ��x2��2x����x2��2x+2��+1������ʽ�ֽ⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��D�ǵȱ���ABC�ı�BC��һ�㣬��ADΪ���������ȱ���ADF��DF��AC���ڵ�N��
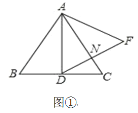
��1����ͼ�٣���AD��BCʱ����˵��DF��AC�����ɣ�
��2����ͼ�ڣ�����D��BC���ƶ�ʱ����ADΪ�����������ȱ���ADE��DE��AB���ڵ�M�������߶�AM��AN��ʲô������ϵ����˵��������ɣ�
��3���ڣ�2���Ļ����ϣ����ȱ���ABC�ı߳�Ϊ2��ֱ��д��DM+DN����Сֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com