
【题目】在平面直角坐标系中,抛物线y=﹣x2+bx+c经过点A、B,C,已知A(﹣1,0),C(0,3).
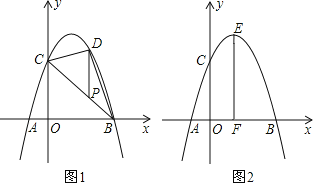
(1)求抛物线的解析式;
(2)如图1,P为线段BC上一动点,过点P作y轴的平行线,交抛物线于点D,是否存在这样的P点,使线段PD的长有最大值?若存在,求出这个最大值;若不存在,请说明理由;
(3)如图2,抛物线的顶点为E,EF⊥x轴于点F,N是直线EF上一动点,M(m,0)是x轴一个动点,请直接写出CN+MN+![]() MB的最小值以及此时点M、N的坐标,直接写出结果不必说明理由.
MB的最小值以及此时点M、N的坐标,直接写出结果不必说明理由.
【答案】(1)y=﹣x2+2x+3;(2)存在,PD最大值为![]() ;(3)
;(3)![]() ,N(1,
,N(1,![]() ),M(
),M(![]() ,0).
,0).
【解析】
(1)y=﹣x2+bx+c经过点C,则c=3,将点A的坐标代入抛物线表达式:y=﹣x2+bx+3,即可求解;
(2)设点D(x,﹣x2+2x+3),则点P(x,﹣x+3),则PD=(﹣x2+2x+3)﹣(﹣x+3)=﹣x2+3x,即可求解;
(3)过点B作倾斜角为30°的直线BH,过点C作CH⊥BH交于点H,CH交对称轴于点N,交x轴于点M,则点M、N为所求,即可求解.
(1)y=﹣x2+bx+c经过点C,则c=3,
将点A的坐标代入抛物线表达式:y=﹣x2+bx+3,得:0=-1-b+3,解得:b=2,
抛物线的表达式为:y=﹣x2+2x+3;
(2)存在,理由:
令y=0,得:﹣x2+2x+3=0,解得:x=﹣1或3,故点B(3,0),
设直线BC为y=kx+b,将点B、C的坐标代入得:
![]() ,解得:
,解得:![]() .
.
∴直线BC的表达式为:y=﹣x+3,
设点D(x,﹣x2+2x+3),则点P(x,﹣x+3),
则PD=(﹣x2+2x+3)﹣(﹣x+3)=﹣x2+3x=![]() ,
,
当x![]() 时,PD最大值为:
时,PD最大值为:![]() ;
;
(3)过点B作倾斜角为30°的直线BH,过点C作CH⊥BH交于点H,CH交对称轴于点N,交x轴于点M,则点M、N为所求.
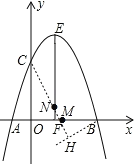
∵∠ABH=30°,∠MHB=90°,∴∠CMO=∠BMH=90°-30°=60°.
∵∠COB=90°,∴∠COM=30°,∴OC=![]() OM.
OM.
∵OC=3,∴OM=![]() ,
,
∴M(![]() ,0),CM=2OM=
,0),CM=2OM=![]() ,MF=OM-OF=
,MF=OM-OF=![]() ,MB=OB-OM=
,MB=OB-OM=![]() .
.
∵∠FMN=60°,∴tan∠FMN=![]() ,∴
,∴![]() ,
,
∴NF=![]() ,∴N(1,
,∴N(1,![]() ).
).
CN+MN![]() MB的最小值=CM
MB的最小值=CM![]() MB=
MB=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,∠ABD=∠BCD=90°,ABCD=BCBD,BM∥CD交AD于点M.连接CM交DB于点N.
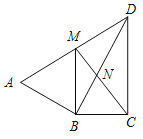
(1)求证:△ABD∽△BCD;
(2)若CD=6,AD=8,求MC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.小明所在的篮球队每月只参加一场比赛,共参加13场,则他参加的比赛中至少有两场比赛的举办月份相同
B.一次抽奖活动的中奖率是![]() ,那么抽100次必然会中一次奖
,那么抽100次必然会中一次奖
C.2019年11月29日是晴天,是必然事件
D.张老师从一个由2名男生和3名女生组成的小组中随机叫一名学生,叫到男生的可能性大于叫到女生的可能性
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市开展早市促销活动,为早到的顾客准备一份简易早餐,餐品为四样A:菜包、B:面包、C:鸡蛋、D:油条.超市约定:随机发放,早餐一人一份,一份两样,一样一个.
(1)按约定,“某顾客在该天早餐得到两个鸡蛋”是 事件(填“随机”、“必然”或“不可能”);
(2)请用列表或画树状图的方法,求出某顾客该天早餐刚好得到菜包和油条的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“植树节”期间,小王、小李两人想通过摸球的方式来决定谁去参加学校植树活动,规则如下:在两个盒子内分别装入标有数字1,2,3,4的四个和标有数字1,2,3的三个完全相同的小球,分别从两个盒子中各摸出一个球,如果所摸出的球上的数字之和小于5,那么小王去,否则就是小李去.
(1)用树状图或列表法求出小王去的概率;
(2)小李说:“这种规则不公平”,你认同他的说法吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.如图,圆柱底面半径为![]() ,高为
,高为![]() ,点
,点![]() 分别是圆柱两底面圆周上的点,且
分别是圆柱两底面圆周上的点,且![]() 、
、![]() 在同一母线上,用一棉线从
在同一母线上,用一棉线从![]() 顺着圆柱侧面绕3圈到
顺着圆柱侧面绕3圈到![]() ,求棉线最短为_________
,求棉线最短为_________![]() 。
。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】兴隆商场将进价为8元的某小商品按每件10元出售,每天可以售出140件,该小商品每件涨1元,其销量就会减少10件.求商场在进货量最小的情况下,该小商品每件销售价应为多少元时,每天的利润为600元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某型号新能源纯电动汽车充满电后,蓄电池剩余电量![]() (千瓦时)关于已行驶路程
(千瓦时)关于已行驶路程![]() (千米)的函数图象.下列说法错误的是( )
(千米)的函数图象.下列说法错误的是( )
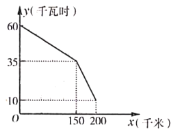
A.该汽车的蓄电池充满电时,电量是60千瓦时
B.蓄电池剩余电量为35千瓦时,汽车已行驶了150千米
C.当汽车已行驶180千米时,蓄电池的剩余电量为20千瓦时
D.25千瓦时的电量,汽车能行使![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
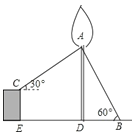
【题目】如图,为了固定一棵珍贵的古树AD,在树干A处向地面引钢管AB,与地面夹角为60,向高1.5m的建筑物CE引钢管AC,与水平面夹角为30,建筑物CE离古树的距离ED为6m,求钢管AB的长.(结果保留整数,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com