
【题目】(1)如图,AC平分∠DAB,∠DCA=∠DAC,试说明AB与CD的位置关系,并予以说明。

(2)如图,在(1)的结论下,AB的下方两点E,F满足:BF平分∠ABE,DF平分∠CDE,若∠DFB=20°,∠CDE=70°,求∠ABE的度数。

【答案】(1)AB∥CD(2)30°
【解析】分析:(1)先由图形可猜测AB∥CD,要证明AB∥CD,只要证明∠2=∠3,再运用角平分线以及∠1=∠2即可求解;
(2)过F作FM∥CD,运用平行线的传递性可得FM∥CD∥AB,由角平分线的定义可得![]() 再运用平行线的性质可得
再运用平行线的性质可得![]() 进而得出∠1=15°,进而求解即可.
进而得出∠1=15°,进而求解即可.
详解:(1)AB∥CD.

证明:∵AC平分∠DAB,
∴∠1=∠3,
又∵∠1=∠2,
∴∠2=∠3,
∴AB∥CD.
(2)过F作FM∥CD,

∵CD∥AB,
∴FM∥CD∥AB,
∵∠CDE=70°,DF平分∠CDE,
∴∠CDF=35°,
∵CD∥FM,
∴![]()
又![]()
∴∠1=15°,
又AB∥FM,
∴∠2=∠1=15°,
又BF平分∠ABE,
∴![]()


科目:初中数学 来源: 题型:
【题目】某校八年级学生在学习《数据的分析》后,进行了检测,现将该校八(1)班学生的成绩统计如下表,并绘制成条形统计图(不完整). 
分数(分) | 人数(人) |
68 | 4 |
78 | 7 |
80 | 3 |
88 | 5 |
90 | 10 |
96 | 6 |
100 | 5 |
(1)补全条形统计图;
(2)该班学生成绩的平均数为86.85分,写出该班学生成绩的中位数和众数;
(3)该校八年级共有学生500名,估计有多少学生的成绩在96分以上(含96分)?
(4)小明的成绩为88分,他的成绩如何,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道:“两边及其中一边的对角分别相等的两个三角形不一定全等”.但是,小亮发现:当这两个三角形都是锐角三角形时,它们会全等,除小亮的发现之外,当这两个三角形都是 时,它们也会全等;当这两个三角形其中一个三角形是锐角三角形,另一个是 时,它们一定不全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,直线l3和直线l1、l2交于点C和D,在直线l3上有点P(点P与点C、D不重合),点A在直线l1上,点B在直线l2上。
(1)如果点P在C、D之间运动时,试说明∠1+∠3=∠2;
(2)如果点P在直线l1的上方运动时,试探索∠1,∠2,∠3之间的关系又是如何?
(3)如果点P在直线l2的下方运动时,试探索∠PAC,∠PBD,∠APB之间的关系又是如何? (直接写出结论)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是以BC为直径的△ABC的外接圆,OP∥AC,且与BC的垂线交于点P,OP交AB于点D,BC、PA的延长线交于点E. 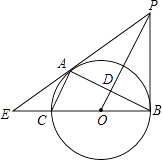
(1)求证:PA是⊙O的切线;
(2)若sinE= ![]() ,PA=6,求AC的长.
,PA=6,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com