

分析 (1)直接利用正弦定理和余弦定理即可得出结论;
(2)方法1、利用正弦定理得出三角形的面积公式,再利用等边三角形的性质即可得出结论;
方法2、先用正弦定理得出S1,S2,S3,S4,最后用余弦定理即可得出结论.
解答 解:(1)在△DEF中,∠F=60°,∠D、∠E的对边分别是3和8,
∴EF=3,DF=8,
∴S△DEF=$\frac{1}{2}$EF×DFsin∠F=$\frac{1}{2}$×3×8×sin60°=6$\sqrt{3}$,
DE2=EF2+DF2-2EF×DFcos∠F=32+82-2×3×8×cos60°=49,
故答案为:6$\sqrt{3}$,49;
(2)证明:方法1,∵∠ACB=60°,
∴AB2=AC2+BC2-2AC•BCcos60°=AC2+BC2-AC•BC,
两边同时乘以$\frac{1}{2}$sin60°得,$\frac{1}{2}$AB2sin60°=$\frac{1}{2}$AC2sin60°+$\frac{1}{2}$BC2sin60°-$\frac{1}{2}$AC•BCsin60°,
∵△ABC',△BCA',△ACB'是等边三角形,
∴S1=$\frac{1}{2}$AC•BCsin60°,S2=$\frac{1}{2}$AB2sin60°,S3=$\frac{1}{2}$BC2sin60°,S4=$\frac{1}{2}$AC2sin60°,
∴S2=S4+S3-S1,
∴S1+S2=S3+S4,
方法2、令∠A,∠B,∠C的对边分别为a,b,c,
∴S1=$\frac{1}{2}$absin∠C=$\frac{1}{2}$absin60°=$\frac{\sqrt{3}}{4}$ab
∵△ABC',△BCA',△ACB'是等边三角形,
∴S2=$\frac{1}{2}$c•c•sin60°=$\frac{\sqrt{3}}{4}$c2,S3=$\frac{1}{2}$a•a•sin60°=$\frac{\sqrt{3}}{4}$a2,S4=$\frac{1}{2}$b•b•sin60°=$\frac{\sqrt{3}}{4}$b2,
∴S1+S2=$\frac{\sqrt{3}}{4}$(ab+c2),S3+S4=$\frac{\sqrt{3}}{4}$(a2+b2),
∵c2=a2+b2-2ab•cos∠C=a2+b2-2ab•cos60°,
∴a2+b2=c2+ab,
∴S1+S2=S3+S4.
点评 此题是三角形综合题,主要考查了新定义的理解和应用,解本题的关键是理解新定义,会用新定义解决问题.


科目:初中数学 来源: 题型:解答题
 如图:
如图:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 品种 项目 | 产量(斤/每棚) | 销售价(元/每斤) | 成本(元/每棚) |
| 香瓜 | 2000 | 12 | 8000 |
| 甜瓜 | 4500 | 3 | 5000 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
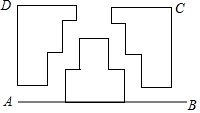 如图,四边形ABCD是一块长方形场地,AB=42米,AD=25米,从A,B两处入口的小路宽都为1米,两小路回合处路宽为2米,其余部分种植草坪,则草坪面积为960平方米.
如图,四边形ABCD是一块长方形场地,AB=42米,AD=25米,从A,B两处入口的小路宽都为1米,两小路回合处路宽为2米,其余部分种植草坪,则草坪面积为960平方米.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2,$\frac{1}{3}$ | B. | 2,1 | C. | 7,3 | D. | 3,3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com