
| A.6cm和8cm | B.10cm和20cm |
| C.8cm和12cm | D.12cm和32cm |
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
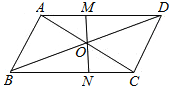
 中,点
中,点 分别为边
分别为边 的中点,
的中点, 相交于点
相交于点 ,则可得结论:①
,则可得结论:① ;②
;② .(不需要证明)
.(不需要证明) 不是正方形
不是正方形 的边
的边 的中点,但满足
的中点,但满足 ,则上面的结论①,②是否仍然成立?(请直接回答“成立”或“不成立”)
,则上面的结论①,②是否仍然成立?(请直接回答“成立”或“不成立”) 分别在正方形
分别在正方形 的边
的边 的延长线和
的延长线和 的延长线上,且
的延长线上,且 ,此时上面的结论1,2是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由.
,此时上面的结论1,2是否仍然成立?若成立,请写出证明过程,若不成立,请说明理由. 和
和 ,若点
,若点 分别为
分别为 的中点,请判断四边形
的中点,请判断四边形 是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.
是“矩形、菱形、正方形、等腰梯形”中的哪一种?并写出证明过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com