
【题目】如图,已知⊙O的直径AB垂直于弦CD于点E,过C点作CG∥AD交AB的延长线于点G,连接CO并延长交AD于点F,且CF⊥AD.
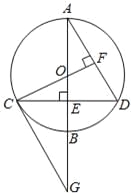
(1)试问:CG是⊙O的切线吗?说明理由;
(2)请证明:E是OB的中点;
(3)若AB=8,求CD的长.
【答案】(1) CG是⊙O的切线,理由见解析;(2)证明见解析;(3)![]() .
.
【解析】试题分析:(1)已知点C在圆上,根据平行线的性质可得∠FCG=90°,即OC⊥CG;故CG是⊙O的切线.
(2)方法比较多,应通过等边三角形的性质或三角形全等的思路来考虑;
(3)Rt△OCE中,有三角函数的定义,可得CE=OE×cot30°,故代入OE=2可得CE的长.
试题解析:(1)CG是⊙O的切线.
理由如下:
∵CG∥AD,
∵CF⊥AD,
∴OC⊥CG.
∴CG是⊙O的切线;
(2)第一种方法:连接AC,如图,
∵CF⊥AD,AE⊥CD且CF,AE过圆心O,
∴![]() .
.
∴AC=AD=CD.
∴△ACD是等边三角形.
在Rt△COE中,
∴OE=![]() OB.
OB.
∴点E为OB的中点.
![]() .
.
∵AE⊥CD,且AE过圆心O,
∴CE=DE.
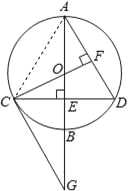
(3)∵AB=8,
∴OC=![]() AB=4.
AB=4.
又∵BE=OE,
∴OE=2.
∴CE=OE×cot30°=![]() .
.
∵AB⊥CD,
∴CD=2CE=![]() .
.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:初中数学 来源: 题型:
【题目】对于二次函数y=3(x-1)2+2的图象,下列说法正确的是( )
A. 开口向下 B. 对称轴是直线x=-1
C. 顶点坐标是(1,2) D. 与x轴有两个交点
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°
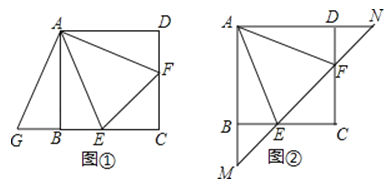
(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;
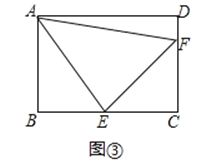
(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将函数y=2x2向左平移2个单位,再向下平移3个单位得到的新函数是( )
A. y=2(x+2)2+3 B. y=2(x﹣2)2+3 C. y=2(x+2)2﹣3 D. y=2(x﹣2)2﹣3
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com