
 如图,抛物线y=ax2+bx+2与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C,与过点C且平行于x轴的直线交于另一点D.
如图,抛物线y=ax2+bx+2与x轴交于A(-1,0)、B(4,0)两点,与y轴交于点C,与过点C且平行于x轴的直线交于另一点D.分析 (1)用待定系数法可得出抛物线的解析式,令y=2可得出点D的坐标;
(2)可先求得CD的长,由△CDP的面积可求得P到CD的距离,可求得P点的纵坐标,再代入抛物线解析式可求得P点坐标;
(3)分两种情况进行讨论,①当AE为一边时,AE∥PD,②当AE为对角线时,根据平行四边形对顶点到另一条对角线距离相等,求解点P坐标.
解答 解:(1)∵抛物线y=ax2+bx+2经过A(-1,0),B(4,0)两点,
∴$\left\{\begin{array}{l}{a-b+2=0}\\{16a+4b+2=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{2}}\\{b=\frac{3}{2}}\end{array}\right.$,
∴y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2;
当y=2时,-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=2,解得:x1=3,x2=0(舍去),
即:点D坐标为(3,2);
(2)由(1)可知C(0,2),D(3,2),
∴CD=3,
设P到CD的距离为h,
∴S△CDP=$\frac{1}{2}$CD•h,
∴$\frac{1}{2}$×3h=$\frac{9}{2}$,解得h=3,
设P点纵坐标为y,则h=|y-2|=3,
解得y=5或y=-1,
∵y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=-$\frac{1}{2}$(x-$\frac{3}{2}$)2+3$\frac{1}{8}$,
∴其最大值为3$\frac{1}{8}$,∴y=5舍去,
当y=-1时,则有-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=-1,解得x=$\frac{3±\sqrt{33}}{2}$,
此时P点坐标为($\frac{3+\sqrt{33}}{2}$,-1)或($\frac{3-\sqrt{33}}{2}$),
综上可知存在满足条件的P点,其坐标为($\frac{3+\sqrt{33}}{2}$,-1)或($\frac{3-\sqrt{33}}{2}$);
(3)A,E两点都在x轴上,AE有两种可能:
①当AE为一边时,AE∥PD,
∴P1(0,2),
②当AE为对角线时,根据平行四边形对顶点到另一条对角线距离相等,
可知P点、D点到直线AE(即x轴)的距离相等,
∴P点的纵坐标为-2,
代入抛物线的解析式:-$\frac{1}{2}$x2+$\frac{3}{2}$x+2=-2,解得:x1=$\frac{3+\sqrt{41}}{2}$,x2=$\frac{3-\sqrt{41}}{2}$,
∴P点的坐标为($\frac{3-\sqrt{41}}{2}$,-2),($\frac{3+\sqrt{41}}{2}$,-2),
综上所述存在满足条件的P点,其坐标为(0,2)或($\frac{3-\sqrt{41}}{2}$,-2)或($\frac{3+\sqrt{41}}{2}$,-2).
点评 此题考查了二次函数的综合应用,综合考查了待定系数法求函数解析式、平行四边形的性质等知识,解答此类题目要求我们能将所学的知识融会贯通,属于中考常涉及的题目,同学们一定要留意.


科目:初中数学 来源: 题型:解答题
 小军利用一张圆心角为90°,半径为20cm的扇形皮纸制作了一顶圆锥形纸帽(如下面的示意图),按照1:5的比例尺画出纸帽的三视图并标注数据.
小军利用一张圆心角为90°,半径为20cm的扇形皮纸制作了一顶圆锥形纸帽(如下面的示意图),按照1:5的比例尺画出纸帽的三视图并标注数据.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某公园有一座雕塑D,在北门B的正南方向,BD为100米,小树林A在北门的南偏西60°方向,荷花池C在北门B的东南方向,已知A,D,C三点在同一条直线上且BD⊥AC:
某公园有一座雕塑D,在北门B的正南方向,BD为100米,小树林A在北门的南偏西60°方向,荷花池C在北门B的东南方向,已知A,D,C三点在同一条直线上且BD⊥AC:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
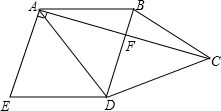 如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC
如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com