
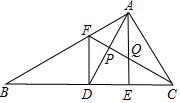
 如图,D为△ABC中边BC中点,E为CD上一点,将△ACE沿AE折叠时C与D重合,F为AB上一点,FB=FC,FC与AD、AE分别交于P、Q点,下列结论
如图,D为△ABC中边BC中点,E为CD上一点,将△ACE沿AE折叠时C与D重合,F为AB上一点,FB=FC,FC与AD、AE分别交于P、Q点,下列结论分析 ①正确.由DF⊥BC,AE⊥BC,即可推出DF∥AE.
②正确.只要证明DF=AQ即可解决问题.
③错误.如图2中,当∠AFQ设钝角是,AQ>AF,即DF>AF,故③错误.
④正确.由△AFP∽△CFA,可得AF2=FP•FC,时PF=PQ=a,则FQ=QC=2a,推出AF2=4a2,推出AF=2a,PC=3a,由此即可判断.
解答 解:∵FB=FC,D为△ABC中边BC中点,
∴DF⊥BC,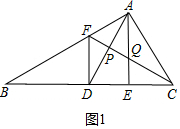
∵将△ACE沿AE折叠时C与D重合,
∴AE⊥BC,
∴AE∥DF;故①正确;
∵BD=CD,DE=CE,
∴DE=CE=$\frac{1}{2}$BD,
∵DF∥AE,
∴$\frac{DF}{AE}$=$\frac{BD}{BE}$=$\frac{2}{3}$,$\frac{QE}{DF}$=$\frac{1}{2}$,
∴AE=$\frac{3}{2}$DF,QE=$\frac{1}{2}$DF,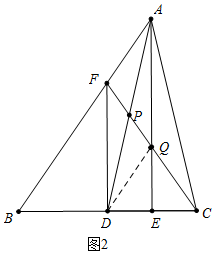
∴$\frac{AE}{QE}$=3,∴QE=$\frac{1}{2}$AQ,
∴DF=AQ,
在△APQ与△DPF中,
解题的关键是灵活运用所学知识解决问题,$\left\{\begin{array}{l}{∠QAP=∠FDP}\\{∠APQ=∠DPF}\\{DF=AQ}\end{array}\right.$,
∴△APQ≌△DPF,故②正确;
如图2中,当∠AFQ设钝角是,AQ>AF,即DF>AF,故③错误.
连接DQ,易证四边形AFDQ是平行四边形,
∴AF∥DQ,
∴∠FAP=∠ADQ,
∵∠ADC=∠ACD,∠QDC=∠QCE,
∴∠ADQ=∠ACF=∠FAP,
∵∠AFP=∠CFA,
∴△AFP∽△CFA,可得AF2=FP•FC,时PF=PQ=a,则FQ=QC=2a,
∴AF2=4a2,
∴AF=2a,PC=3a,
∴$\frac{AF}{CP}=\frac{2}{3}$,故④正确,
故答案为①②④.
点评 本题考查翻折变换、全等三角形的判定和性质、线段的垂直平分线的性质定理、平行四边形的判定和性质.相似三角形的判定和性质等知识,本题的突破点设证明DF=AQ,学会利用参数解决问题,属于中考填空题中的压轴题.


科目:初中数学 来源: 题型:解答题
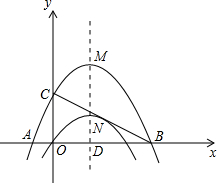 已知:如图二次函数y=-$\frac{1}{4}$x2+bx+c图象经过原点O,图象顶点为N,对称轴ND为直线x=3.
已知:如图二次函数y=-$\frac{1}{4}$x2+bx+c图象经过原点O,图象顶点为N,对称轴ND为直线x=3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
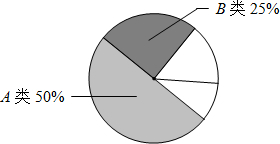 期末考试后,某市第一中学为了解本校九年级学生期末考试数学学科成绩情况,决定对该年级学生数学学科期末考试成绩进行抽样分析,已知九年级共有12个班,每班48名学生,请按要求回答下列问题:
期末考试后,某市第一中学为了解本校九年级学生期末考试数学学科成绩情况,决定对该年级学生数学学科期末考试成绩进行抽样分析,已知九年级共有12个班,每班48名学生,请按要求回答下列问题:| 成绩(单位:分) | 频数 | 频率 |
| A类(80~100) | $\frac{1}{2}$ | |
| B类(60~79) | $\frac{1}{4}$ | |
| C类(40~59) | 8 | $\frac{1}{6}$ |
| D类(0~39) | 4 | $\frac{1}{12}$ |
| 学校 | 平均数(分) | 极差(分) | 方差 | A、B类的频率和 |
| 第一中学 | 71 | 52 | 432 | 0.75 |
| 第二中学 | 71 | 80 | 497 | 0.82 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
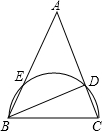 如图,在△ABC中,AB=AC,以BC为直径画半圆交AB于E,交AC于D,$\widehat{CD}$的度数为40°,则∠A的度数是( )
如图,在△ABC中,AB=AC,以BC为直径画半圆交AB于E,交AC于D,$\widehat{CD}$的度数为40°,则∠A的度数是( )| A. | 40° | B. | 70° | C. | 50° | D. | 20° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
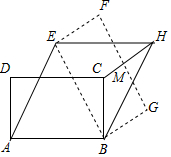 如图,矩形ABCD中,AB=3,AD=$\sqrt{3}$,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM=( )
如图,矩形ABCD中,AB=3,AD=$\sqrt{3}$,将矩形ABCD绕点B按顺时针方向旋转后得到矩形EBGF,此时恰好四边形AEHB为菱形,连接CH交FG于点M,则HM=( )| A. | $\frac{1}{2}$ | B. | 1 | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
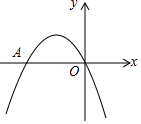 如图,二次函数y=-x2+bx+c的图象经过坐标原点,与x轴的另一个交点为A(-2,0).
如图,二次函数y=-x2+bx+c的图象经过坐标原点,与x轴的另一个交点为A(-2,0).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com