练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    如图，在矩形ABCD中，tan∠BAC=3，AD=18，求矩形ABCD的面积．
    考点：解直角三角形
    专题：
    分析：先根据四边形ABCD是矩形可知AD=BC，∠ABC=90°，再由tan∠BAC=3可设AB=x，则BC=3x，再根据AD=18求出x的值，根据矩形的面积即可得出结论．
    解答：解：∵四边形ABCD是矩形，
    ∴AD=BC=18，∠ABC=90°，
    ∵tan∠BAC=3，
    ∴设AB=x，则BC=3x，
    ∴3x=18，解得x=6，
    ∴AB=6，BC=18，
    ∴S矩形ABCD=6×18=108．
    点评：本题考查的是解直角三角形，熟知锐角三角函数的定义及矩形的性质是解答此题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    -（-
    1
    2
    ）的相反数是（　　）
    A、
    1
    2
    B、-
    1
    2
    C、2
    D、-2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

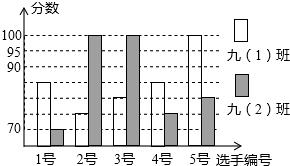    某中学开展“我的中国梦”演讲比赛活动，九（1）、九（2）班根据初赛成绩各选出5名选手参加复赛，两个班各选出的5名选手的复赛成绩（满分为100分）如下图所示．
    （1）根据如图，分别求出两班复赛的平均成绩和方差；
    （2）根据（1）的计算结果，分析哪个班级5名选手的复赛成绩波动小？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    现有乱成一团的铁丝和铜丝各一捆（可以称出每捆质量）．已知铁丝和铜丝的截面半径分别为r1cm和r2cm，请你设计一种方案，不用直接测量长度，就能计算这捆铁丝和这捆铜丝的长度差（注：铁的密度约为8g/cm3．铜的密度约为9g/cm3）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    先化简，再求值：
    （1）化简：（2x2-
    1
    2
    +3x）-4（x-x2+
    1
    2
    ）
    （2）化简：
    1
    2
    x-2(x-
    1
    3
    y2)-(-
    3
    2
    x+
    1
    3
    y2)
    （3）先化简再求值：5（3a2b-ab2）-2（ab2+3a2b），其中a=-
    1
    2
    ，b=
    1
    3
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

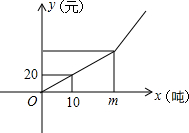    某市制定了一套节约用水的管理措施，其中规定每月用水量超过m（吨）时，超过部分每吨加收环境保护费
    m
    100
    元．如图反映了每月收取的水费y（元）与每月用水量x（吨）之间的函数关系，表是一家酒店四、五两月用水量及缴费情况．
    月份 用水量x（吨） 水费y（元）
    四月 30 60
    五月 80 172
    （1）求m的值；
    （2）求y与x之间的函数关系式，并写出相应的取值范围；
    （3）在（1）、（2）的条件下，若将计费周期调整为2个月，并规定2个月总用水量超过m（吨）时，超过部分每吨加收环境保护费
    m
    200
    元，则四、五月份共缴费多少元？
    （4）在上述条件下，若每个月用水都为n吨，就n的不同取值范围分析“单月收费”和“双月收费”哪种方式对用户更合算？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，在△ABC中，AB=AC，BC=20，△ABC的面积为
    100
    3
    		3
    ，求tanB．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    一条排水管的截面如图所示，已知水面宽AB=10cm，截面圆⊙O的半径OC⊥AB于D，且OD：DC=3：2，求⊙O的直径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    如图，一块三角形铁皮，其中∠B=30°，∠C=45°，AC=12
    		2
    cm，工人师傅利用这块铁皮做了一个侧面积最大的圆锥，求这个圆锥的底面直径．

    查看答案和解析>>

    同步练习册答案