
【题目】如图,在正方形ABCD中,E、F分别是BC、CD边上的点,∠EAF=45°.
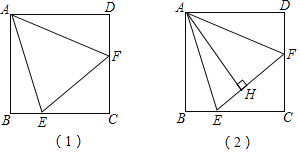
(1)如图(1),试判断EF,BE,DF间的数量关系,并说明理由;
(2)如图(2),若AH⊥EF于点H,试判断线段AH与AB的数量关系,并说明理由.
【答案】(1)BE+DF=EF理由见解析;(2)AH=AB,理由见解析
【解析】
(1)延长FD到G,使DG=BE,连接AG,证△GDA≌△EBA,△GAF≌△EAF,根据全等三角形的性质得出GD+DF=BE+DF=EF进而求出即可;
(2)把△ADF绕点A顺时针旋转90°得到△ABQ,如图,根据旋转的性质得AQ=AF,∠FAQ=90°,∠ABQ=∠D=90°,则可判断点Q在CB的延长线上,由∠EAF=45°得到∠QAE=90°﹣∠EAF=45°,然后根据“SAS”判断△AEQ≌△AEF,得到EQ=FE,再根据全等三角形对应边上的高相等得到结论.
解:(1)BE+DF=EF;
理由如下:
如图1,延长FD到G,使DG=BE,连接AG,

∵在△GDA和△EBA中,
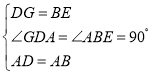 ,
,
∴△GDA≌△EBA(SAS),
∴AG=AE,∠GAD=∠EAB,
故∠GAF=45°,
在△GAF和△EAF中,
∵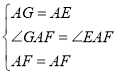 ,
,
∴△GAF≌△EAF(SAS),
∴GF=EF,
即GD+DF=BE+DF=EF;
(2)AH=AB,
理由如下:
∵四边形ABCD为正方形,
∴AB=AD,∠BAD=90°,
∴把△ADF绕点A顺时针旋转90°得到△ABQ,如图2,

∴AQ=AF,∠FAQ=90°,∠ABQ=∠D=90°,
而∠ABC=90°,
∴点Q在CB的延长线上,
∵∠EAF=45°,
∴∠QAE=90°﹣∠EAF=45°,
∴∠EAF=∠QAE,
在△AEQ和△AEF中,
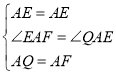 ,
,
∴△AEQ≌△AEF(SAS),
∴EQ=EF,
∵AB⊥EQ,AH⊥FE,
∴AB=AH.


 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:初中数学 来源: 题型:
【题目】已知一次函数![]() ,二次函数
,二次函数![]() (其中m>4).
(其中m>4).
(1)求二次函数图象的顶点坐标(用含m的代数式表示);
(2)利用函数图象解决下列问题:
①若![]() ,求当
,求当![]() 且
且![]() ≤0时,自变量
≤0时,自变量![]() 的取值范围;
的取值范围;
②如果满足![]() 且
且![]() ≤0时自变量
≤0时自变量![]() 的取值范围内有且只有一个整数,直接写出
的取值范围内有且只有一个整数,直接写出![]() 的取值范围.
的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在宽20米,长32米的矩形耕地上,修筑同样宽的三条路(两条纵向,一条横向,并且横向与纵向互相垂直),把这块耕地分成大小相等的六块试验田,要使试验田的面积是570平方米,问道路应该多宽?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,点D在BC上,BD=6,CD=2,点P′是AB上的动点,则PC+PD的最小值是( )
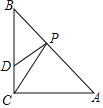
A.7B.8C.9D.10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各组数:(3,4,5),(5,12,13),(7,24,25),(9,40,41),…,由此可发现:![]() ,
,![]() ,
,![]() ,…,请写出第6个数组:__.
,…,请写出第6个数组:__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴交于点A(﹣1,0)和点B,与y轴交于点C,点C关于抛物线对称轴的对称点为点D,抛物线顶点为H(1,2).
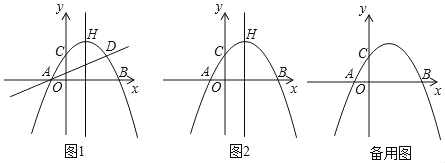
(1)求抛物线的解析式;
(2)点P为直线AD上方抛物线的对称轴上一动点,连接PA,PD.当S△PAD=3,若在x轴上存在一动点Q,使PQ+![]() QB最小,求此时点Q的坐标及PQ+
QB最小,求此时点Q的坐标及PQ+![]() QB的最小值;
QB的最小值;
(3)若点E为抛物线上的动点,点G,F为平面内的点,以BE为边构造以B,E,F,G为顶点的正方形,当顶点F或者G恰好落在y轴上时,求点E的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
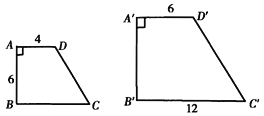
【题目】已知:如图,梯形ABCD与梯形A′B′C′D′相似,AD∥BC,A′D′∥B′C′,∠A=∠A′.AD=4,A′D′=6,AB=6,B′C′=12.求:
(1)梯形ABCD与梯形A′B′C′D′的相似比k;
(2)A′B′和BC的长;
(3)D′C′∶DC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司购买了一批![]() 、
、![]() 型芯片,其中
型芯片,其中![]() 型芯片的单价比
型芯片的单价比![]() 型芯片的单价少9元,已知该公司用3120元购买
型芯片的单价少9元,已知该公司用3120元购买![]() 型芯片的条数与用4200元购买
型芯片的条数与用4200元购买![]() 型芯片的条数相等.
型芯片的条数相等.
(1)求该公司购买的![]() 、
、![]() 型芯片的单价各是多少元?
型芯片的单价各是多少元?
(2)若两种芯片共购买了200条,且购买的总费用为6280元,求购买了多少条![]() 型芯片?
型芯片?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面真角坐标系中,点A.B的坐标分别为A(a,0),B(b,0),且a,b满足|a+1|+![]() =0,点C的坐标为(0,3).
=0,点C的坐标为(0,3).
(1)求a,b的值及S△ABC;
(2)若点M在x轴上,且S△ACM=![]() S△ABC,试求点M的坐标.
S△ABC,试求点M的坐标.
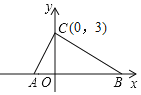
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com