
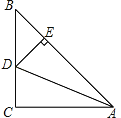
【题目】如图,在△ABC中,∠C=90°,AC=BC,AD平分∠BAC交BC于点D,DE⊥AB于点E,若△BDE的周长是6,则AB= ,AC= .
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
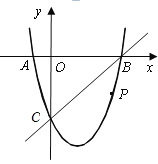
(1)求二次函数解析式;
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形![]() .是否存在点P,使四边形
.是否存在点P,使四边形![]() 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD中,M、N是BD的三等分点,连接CM并延长交AB于点E,连接EN并延长交CD于点F,以下结论:
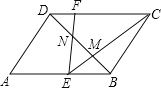
①E为AB的中点;
②FC=4DF;
③S△ECF=![]() ;
;
④当CE⊥BD时,△DFN是等腰三角形.
其中一定正确的是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年的“六·一”儿童节是个星期五,某校学生会在初一年级进行了学生对学校作息安排的三种期望(全天休息、半天休息、全天上课)的抽样调查,并把调查结果绘成了如图1、2的统计图,已知此次被调查的男、女学生人数相同.根据图中信息,下列判断:①在被调查的学生中,期望全天休息的人数占53%;②本次调查了200名学生;③在被调查的学生中,有30%的女生期望休息半天;④若该校现有初一学生900人,根据调查结果估计期望至少休息半天的学生超过了720人.其中正确的判断有
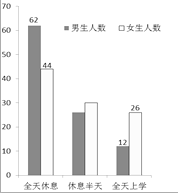
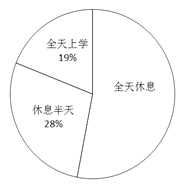
图1 图2
A. 4个. B. 3个. C. 2个. D. 1个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,4),B(1,2),C(5,1)是平面直角坐标系中的三点.
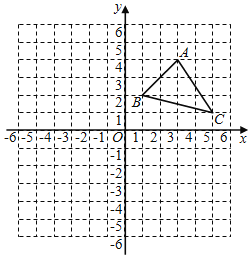
(1)请画出△ABC关于y轴对称的△A1B1C1;
(2)分别写出点A1,B1,C1的坐标;
(3)连接AA1,BB1,求四边形AA1B1B的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
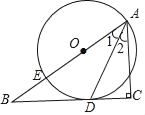
【题目】如图,已知点E在直角△ABC的斜边AB上,以AE为直径的⊙O与直角边BC相交于点D,AD平分∠BAC.
(1)求证,BC是⊙O的切线.
(2)若BE=2,BD=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
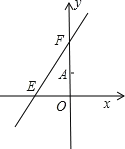
【题目】如图,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴相交于点
轴相交于点![]() 和点
和点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(1)求![]() 的值;
的值;
(2)若点![]() 是第二象限内的直线上的一个动点,当点
是第二象限内的直线上的一个动点,当点![]() 运动过程中,试写出
运动过程中,试写出![]() 的面积
的面积![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(3)探究:当![]() 运动到什么位置时,
运动到什么位置时,![]() 的面积为
的面积为![]() ,并说明理由.
,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com