
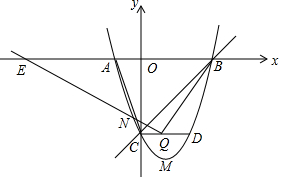
 如图,已知抛物线与x轴交于A(-1,0),B(3,0),与y轴交于C(0,-3),顶点为点M.
如图,已知抛物线与x轴交于A(-1,0),B(3,0),与y轴交于C(0,-3),顶点为点M.分析 (1)设交点式y=a(x+1)(x-3),再把C点坐标代入求出a即可得到抛物线的解析式,然后把一般式化为顶点式可得到点M的坐标;
(2)连接MC,作MF⊥y轴于点F,如图,则点F坐标为(0,-4),先证明△CMF为等腰直角三角形得到MC=$\sqrt{2}$,∠FCM=∠FMC=45°,△OBC为等腰直角三角形得到∠OCB=∠OBC=45°.则∠PCM=90°,过点P作PH⊥y轴于H,如图,根据相似三角形的判定方法当$\frac{PC}{AO}$=$\frac{MC}{CO}$时,△PCM∽△AOC,利用相似比计算出PC=$\frac{\sqrt{2}}{3}$,从而得到PH=CH=$\frac{1}{3}$,则可确定此时点P的坐标为($\frac{1}{3}$,-$\frac{8}{3}$);当$\frac{PC}{CO}$=$\frac{MC}{AO}$时,△PCM∽△COA,用同样方法可确定此时P点坐标为(3,0);
(3)设点E的坐标为(n,0),Q的坐标为(m,-3),先利用对称性得到D(2,-3),利用两点间的距离公式计算出BD=$\sqrt{10}$,再证明△NCQ∽△QDB,利用相似比得到CN=-$\frac{\sqrt{10}}{10}$(m2-2m),根据二次函数的性质可确定此时Q的坐标为(1,-3),然后证明△EQB∽△BDQ,再利用相似比求出BE的长,从而可得到E点坐标.
解答 解:(1)∵抛物线与x轴交于A(-1,0),B(3,0),
∴设抛物线的解析式为y=a(x+1)(x-3).
把(0,-3)代入y=a(x+1)(x-3)得a•1•(-3)=-3,解得a=1,
∴抛物线的解析式为y=(x+1)(x-3),即y=x2-2x-3.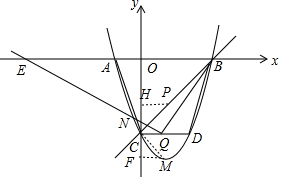
∵y=x2-2x-3=(x-1)2-4,
∴点M的坐标是(1,-4);
(2)连接MC,作MF⊥y轴于点F,如图,则点F坐标为(0,-4).
∵MF=1,CF=-3-(-4)=1,
∴△CMF为等腰直角三角形,
∴MC=$\sqrt{2}$,∠FCM=∠FMC=45°,
∵B(3,0),C(0,-3),
∴OB=OC=3,
∴△OBC为等腰直角三角形,
∴∠OCB=∠OBC=45°.
∴∠MCB=180°-∠OCB-∠FCM=90°,
即∠PCM=90°,
过点P作PH⊥y轴于H,如图,
∵∠PCM=∠AOC,
∴当$\frac{PC}{AO}$=$\frac{MC}{CO}$时,△PCM∽△AOC,即$\frac{PC}{1}$=$\frac{\sqrt{2}}{3}$,解得PC=$\frac{\sqrt{2}}{3}$,
∵∠PCH=45°,
∴PH=CH=$\frac{\sqrt{2}}{2}$PC=$\frac{1}{3}$,
∴OH=OC-CH=3-$\frac{1}{3}$=$\frac{8}{3}$,
∴此时点P的坐标为($\frac{1}{3}$,-$\frac{8}{3}$);
∴当$\frac{PC}{CO}$=$\frac{MC}{AO}$时,△PCM∽△COA,即$\frac{PC}{3}$=$\frac{\sqrt{2}}{1}$,解得PC=3$\sqrt{2}$,
∴PH=CH=$\frac{\sqrt{2}}{2}$PC=3,
∴OH=OC-CH=3-$\frac{1}{3}$=$\frac{8}{3}$,
∴此时点P与点B重合,即P点坐标为(3,0);
综上所述,符合题意的P点坐标为P($\frac{1}{3}$,-$\frac{8}{3}$)或(3,0);
(3)设点E的坐标为(n,0),Q的坐标为(m,-3).
∵CD∥x轴,
∴C点和D点关于直线x=1对称,
∴D(2,-3),
∴BD=$\sqrt{(3-2)^{2}+{3}^{2}}$=$\sqrt{10}$,
∵Q(m,-3),
∴QD=2-m,CQ=m(0≤m≤2),
∵∠BQE=∠BDC,∠EQC+∠BQE=∠BDC+∠QBD,
∴∠EQC=∠QBD,
又由抛物线的轴对称性可知:∠NCQ=∠BDC,
∴△NCQ∽△QDB.
∴$\frac{CN}{QD}$=$\frac{CQ}{BD}$,即$\frac{CN}{2-m}$=$\frac{m}{\sqrt{10}}$,
∴CN=-$\frac{\sqrt{10}}{10}$(m2-2m)=-$\frac{\sqrt{10}}{10}$(m-1)2+$\frac{\sqrt{10}}{10}$,
∴当m=1时,CN有最大值,此时Q的坐标为(1,-3),
∴QG=3,BG=2,QD=1.
∴QB=$\sqrt{(3-1)^{2}+{3}^{2}}$=$\sqrt{13}$,
∵CD∥x轴,
∴∠BEQ=∠NQC=∠QBD,
而∠EBQ=∠BQD.
∴△EQB∽△BDQ.
∴$\frac{BQ}{QD}$=$\frac{EB}{BQ}$,即$\frac{\sqrt{13}}{1}$=$\frac{BE}{\sqrt{13}}$,解得BE=13,
∴OE=BE-OB=13-3=10,
∴E的坐标为(-10,0).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质、等腰直角三角形的性质和相似三角形的判定于性质;会利用待定系数法求二次函数和一次函数解析式;能利用两点间的距离公式和相似计算线段的长;理解坐标与图形性质;会应用分类讨论的思想解决数学问题.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC为直角三角形,∠B=90°,AC边上取一点D,使CD=AB,分别过点C作CE⊥BC,过D作DE⊥AC,CE,DE相交于E.连结AE.
如图,△ABC为直角三角形,∠B=90°,AC边上取一点D,使CD=AB,分别过点C作CE⊥BC,过D作DE⊥AC,CE,DE相交于E.连结AE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com