
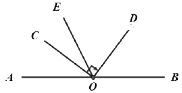
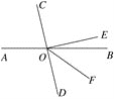
【题目】已知点A、O、B在一条直线上,将射线OC绕O点顺时针方向旋转90°后,得到射线OD,在旋转过程中,射线OC始终在直线AB上方,且OE平分∠AOD.约定,无论∠AOD大小如何,OE都看作是由OA、OD两边形成的最小角的平分线.
(1)如图,当∠AOC=30°时,∠BOD=_________°;
(2)若射线OF平分∠BOC,求∠EOF的度数.
【答案】(1)60;(2)45°或135°
【解析】
(1)根据平角定义即可得出结论;
(2)分两种情况讨论:①当OC、OD都在直线AB上方时;当OC在直线AB上方,OD在直线AB下方时.
(1)∵∠AOC=30°,∠COD=90°,∴∠BOD=180°-∠AOC-∠COD=180°-30°-90°=60°.
(2)分两种情况讨论:
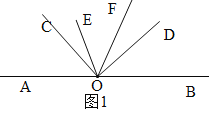
①当OC、OD都在直线AB上方时,如图1.设∠AOC=x,则∠BOC=180°-x.
∵∠COD=90°,∴∠AOD=90°+x,∠BOD=90°-x.
∵OE平分∠AOD,∴∠EOD=![]() ∠AOD=
∠AOD=![]() (90°+x)=45°+0.5x.
(90°+x)=45°+0.5x.
∵OF平分∠BOC,∴∠BOF=![]() ∠BOC=
∠BOC=![]() (180°-x)=90°-0.5x,∴∠FOD=∠BOF-∠BOD=(90°-0.5x)-(90°-x)=0.5x,∴∠EOF=∠EOD-∠DOF=(45°+0.5x)-0.5x=45°.
(180°-x)=90°-0.5x,∴∠FOD=∠BOF-∠BOD=(90°-0.5x)-(90°-x)=0.5x,∴∠EOF=∠EOD-∠DOF=(45°+0.5x)-0.5x=45°.
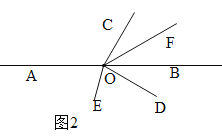
②当OC在直线AB上方,OD在直线AB下方时,如图2.
设∠AOC=x,则∠BOC=180°-x.
∵∠COD=90°,∴∠AOD=360°-90°-x=270°-x,∠BOD=180°-∠AOD=180°-(270°-x)=x-90°.
∵OE平分∠AOD,∴∠EOD=![]() ∠AOD=
∠AOD=![]() (270°-x)=135°-0.5x.
(270°-x)=135°-0.5x.
∵OF平分∠BOC,∴∠BOF=![]() ∠BOC=
∠BOC=![]() (180°-x)=90°-0.5x,∴∠FOD=∠BOF+∠BOD=(90°-0.5x)+(x-90°)=0.5x,∴∠EOF=∠EOD+∠DOF=(135°-0.5x)+0.5x=135°.
(180°-x)=90°-0.5x,∴∠FOD=∠BOF+∠BOD=(90°-0.5x)+(x-90°)=0.5x,∴∠EOF=∠EOD+∠DOF=(135°-0.5x)+0.5x=135°.
综上所述:∠EOF的度数为45°或135°.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,甲、乙、丙三艘轮船从港口O出发,当分别行驶到A,B,C处时,经测量得,甲船位于港口的北偏东43°45′方向,乙船位于港口的北偏东76°35′方向,丙船位于港口的北偏西43°45′方向.
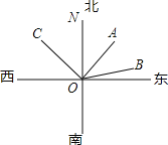
(1)求∠BOC的度数;
(2)求∠AOB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为筹备校庆活动,准备印制一批校庆纪念册,该纪念册每册需要10张8K大小的纸,其中4张为彩色页,6张为黑白页.印制该纪念册的总费用由制版费和印刷费两部分组成,制版费与印数无关,价格为:彩色页300元/张,黑白页50元/张;印刷费与印数的关系见表.
印数a (单位:千册) | 1≤a<5 | 5≤a<10 |
彩色 (单位:元/张) | 2.2 | 2.0 |
黑白(单位:元/张) | 0.7 | 0.6 |
(1)直接写出印制这批纪念册的制版费为多少元;
(2)若印制6千册,那么共需多少费用?
(3)如印制x(1≤x<10)千册,所需费用为y元,请写出y与x之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给下面命题的说理过程填写依据.
已知:如图,直线AB,CD相交于点O,EO⊥CD,垂足为O,OF平分∠BOD,对∠EOF=![]() ∠BOC说明理由.
∠BOC说明理由.
理由:因为∠AOC=∠BOD( ),
∠BOF=![]() ∠BOD( ),
∠BOD( ),
所以∠BOF=![]() ∠AOC( ).
∠AOC( ).
因为∠AOC=180°-∠BOC( ),
所以∠BOF=90°-![]() ∠BOC.
∠BOC.
因为EO⊥CD( ),
所以∠COE=90°( )
因为∠BOE+∠COE=∠BOC( ),
所以∠BOE=∠BOC-∠COE.
所以∠BOE=∠BOC-90°( )
因为∠EOF=∠BOE+∠BOF( )
所以∠EOF=(∠BOC-90°)+(90°![]() ∠BOC)( )
∠BOC)( )
所以∠EOF=![]() ∠BOC.
∠BOC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个用硬纸板制作的长方体包装盒展开图,已知它的底面形状是正方形,高为12cm.
(1)制作这样的包装盒需要多少平方厘米的硬纸板?
(2)若1平方米硬纸板价格为5元,则制作10个这的包装盒需花费多少钱?(不考虑边角损耗)

查看答案和解析>>
科目:初中数学 来源: 题型:
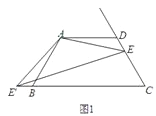
【题目】已知:四边形ABCD中,AD∥BC,AD=AB=CD,∠BAD=120°,点E是射线CD上的一个动点(与C、D不重合),将△ADE绕点A顺时针旋转120°后,得到△ABE',连接EE'.
(1)如图1,∠AEE'= °;
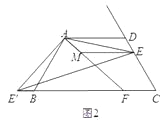
(2)如图2,如果将直线AE绕点A顺时针旋转30°后交直线BC于点F,过点E作EM∥AD交直线AF于点M,写出线段DE、BF、ME之间的数量关系;
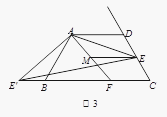
(3)如图3,在(2)的条件下,如果CE=2,AE=![]() ,求ME的长.
,求ME的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=2x-4
(1)画出函数的图象;
(2)判断点A(1,-2),B(2,1)是否在该函数的图象上.
(3)已知点A(-2,b)在该函数图像上,求b值;
查看答案和解析>>
科目:初中数学 来源: 题型:
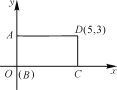
【题目】已知长方形ABCD在平面直角坐标系中的位置如图所示,将长方形ABCD沿x轴向左平移到使点C与坐标原点重合后,再沿y轴向下平移到使点D与坐标原点重合,此时点A的坐标是______,点B的坐标是______,点C的坐标是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
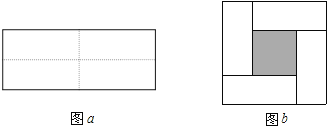
【题目】图a是一个长为2m,宽为2n的长方形,沿图a中虚线用剪刀把它均分成四块小长方形,然后按图b的形状拼成一个正方形.
(1)请用两种不同的方法求图b中阴影部分的面积:
方法1: ____ (只列式,不化简)
方法2: ______ (只列式,不化简)
(2)观察图b,写出代数式(m+n)2,(m-n)2,mn之间的等量关系: ______ ;
(3)根据(2)题中的等量关系,解决如下问题:若a+b=7,ab=5,
则(a-b)2= ______ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com