
 如图,已知二次函数y=x2-2x-3与x轴围成一个封闭图形,则在这个封闭图形内(包括边界),横坐标和纵坐标都是整数的点有( )
如图,已知二次函数y=x2-2x-3与x轴围成一个封闭图形,则在这个封闭图形内(包括边界),横坐标和纵坐标都是整数的点有( )| A. | 13个 | B. | 14个 | C. | 15个 | D. | 16个 |
分析 首先确定A、B的坐标,以及对称轴和顶点坐标,然后根据封闭部分自变量x的取值判断即可.
解答 解:在y=x2-2x-3中令y=0,则x2-2x-3=0,解得:x=-1或3,
则A的坐标是(-1,0),B的坐标是(3,0).
对称轴是x=1.顶点坐标是(1,-4).
当x=-1时,有点(-1,0),当x=0时,函数y=-3,则有(0,0),(0,-1),(0,-2),(0,-3)四个点.
则对称轴左侧有5个点在这个封闭图形内,同理右侧有5个.
对称轴上有(1,0),(1,-1),(1,-2),(1,-3),(1,-4)共5个.
则满足条件的点有15个.
故选C.
点评 本题考查了抛物线与x轴的交点,以及对称轴个顶点坐标的求法,正确满足条件的x的值是关键.


科目:初中数学 来源: 题型:解答题

| 划分次数 | 扇形总个数 |
| 1 | 6 |
| 2 | 11 |
| 3 | 16 |
| 4 | 21 |
| … | … |
| n | 5n+1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
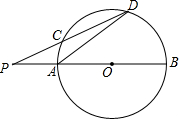 如图,PAB、PCD是⊙O的两条割线,且PAB经过圆心O,若$\widehat{DB}$=$\widehat{DC}$,∠P=24°,则∠ADC=14°.
如图,PAB、PCD是⊙O的两条割线,且PAB经过圆心O,若$\widehat{DB}$=$\widehat{DC}$,∠P=24°,则∠ADC=14°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com