
 某体育用品商场为了推销一种品牌运动服,先做了市场调查,得到数据如下表:
某体育用品商场为了推销一种品牌运动服,先做了市场调查,得到数据如下表:| 卖出价格x(元/件) | 50 | 51 | 52 | 53 |
| 销售量p(件) | 500 | 490 | 480 | 470 |
分析 (1)根据描点易知是一次函数关系,由其中两点利用待定系数法可求关系式;
(2)根据利润的计算方法求关系式;
(3)运用函数的性质求最值.
解答 解:(1)描点如下: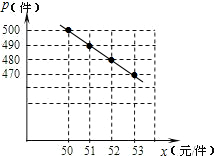
由图象可知p与x成一次函数关系.
设函数关系式为p=kx+b,则:
$\left\{\begin{array}{l}{50k+b=500}\\{51k+b=490}\end{array}\right.$,
解得:k=-10,b=1000,
∴p=-10x+1000;
(2)依题意得:y=px-40p=(-10x+1000)x-40(-10x+1000),
∴y=-10x2+1400x-40000;
(3)由y=-10x2+1400x-40000=-10(x-70)2+9000可知,
当x=70时,y有最大值,最大值为9000元.
答:当卖出价为70时,能获得最大利润,最大利润为9000元.
点评 此题考查了一次函数及二次函数的图象与性质,熟练掌握待定系数法求函数解析式及依据销售问题中利润的相等关系是列函数解析式解题的关键.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:解答题
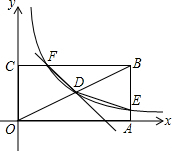 如图,矩形OABC的顶点A,C分别在x,y轴的正半轴上,D为对角线OB的中点,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点D,且与AB、BC分别交于点E,F,点B的坐标为(2$\sqrt{3}$,2).
如图,矩形OABC的顶点A,C分别在x,y轴的正半轴上,D为对角线OB的中点,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点D,且与AB、BC分别交于点E,F,点B的坐标为(2$\sqrt{3}$,2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
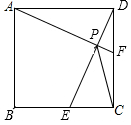 如图,正方形ABCD中,点E为BC的中点,作AF⊥DE交DE、DC分别于P、F点,连PC.
如图,正方形ABCD中,点E为BC的中点,作AF⊥DE交DE、DC分别于P、F点,连PC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 某市准备在一块三条公路围成的平地△ABC上设立一个大型超市,要求超市到三条公路的距离相等,则超市应建在△ABC的( )
某市准备在一块三条公路围成的平地△ABC上设立一个大型超市,要求超市到三条公路的距离相等,则超市应建在△ABC的( )| A. | 两个角的平分线的交点处 | B. | 两边高线的交点处 | ||
| C. | 两边中线的交点处 | D. | 内部即可 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 路程 | +5 | -3 | +10 | -8 | -6 | +12 | -10 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com