练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    1．小华在电话中问小明：“已知一个三角形三边长分别是5，9，12，如何求这个三角形的面积？小明提示说：“可通过作最长边上的高来求解．”小华根据小明的提示作出的图形正确的是（　　）
    A．B．C．D．

    分析 由三角形的三边为4，9，12，可知该三角形为钝角三角形，其最长边上的高在三角形内部，即过最长边所对的角的顶点，作对边的垂线，垂足在最长边上．

    解答 解：∵42+92=97＜122，
    ∴三角形为钝角三角形，
    ∴最长边上的高是过最长边所对的角的顶点，作对边的垂线，垂足在最长边上．
    故选：C．

    点评 本题考查了三角形高的画法．当三角形为锐角三角形时，三条高在三角形内部；当三角形是直角三角形时，两条高是三角形的直角边，一条高在三角形内部；当三角形为钝角三角形时，两条高在三角形外部，一条高在内部．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

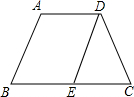    11．如图，等腰梯形ABCD中，AD∥BC，AD=5，∠B=60°，BC=11，且AB∥DE，△DEC的周长是（　　）
    A．21B．20C．19D．18

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．下列多项式中，能用公式a2±2ab+b2=（a±b）2因式分解的是（　　）
    A．x2-xy+y2B．4a2+2ab+b2C．-a2+2ab-b2D．x2-2y-y2

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图，△ABC和△ADE都是等边三角形，且点B，A，E在同一直线上，连接BD交AC于M，连接CE交AD于N，连接MN．
    （1）求证：BD=CE；
    （2）求证：BM=CN；
    （3）求证：MN∥BE．
    （4）若点P，Q分别是BD，CE的中点，试判断△PAQ的形状，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

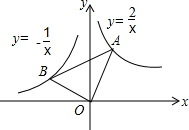    16．如图，在x轴的上方，∠BOA（直角）绕原点O按顺时针方向旋转，若∠BOA的两边分别与函数y=-$\frac{1}{x}$、y=$\frac{2}{x}$的图象交于B、A两点，则△AOB面积的最小值为$\sqrt{2}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．如图，在反比例函数y=$\frac{k}{x}$的图象上有一点A，过A作AC垂直x轴于点C，已知点C的坐标为（1，0），点D与点C关于原点对称，且S△ACD=4，直线AD交双曲线的另一支于点B．
    （1）求k的值；
    （2）求△BCD的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．下列各式计算正确的是（　　）
    A．3x2•4x3=12x6B．3x3•（-2x2）=-6x5C．（-3x2）•（5x3）=15x5D．（-2x）2•（-3x）3=6x5

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．下列说法中：①-2是相反数；②2是相反数；③-2是2的相反数；④-2和2互为相反数．其中正确的有（　　）
    A．1个B．2个C．3个D．4个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    11．△ABC中，∠ACB=90°，CA=CB，D是AB的中点，∠APC=90°，PA≠PC，连接PD．
    （1）如图1，当点P在△ABC内时，求证：PA-PC=$\sqrt{2}$PD．
    （2）当点P在△ABC外，且PA＜PC时，试探究PC、PA、PD之间的数量关系．
    （3）如图3，当PA＜PC，AB=$10\sqrt{2}$，PD=7$\sqrt{2}$时，求PB的长．

    查看答案和解析>>

    同步练习册答案