
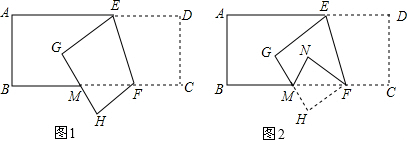
分析 (1)如图1,利用平行线的性质得∠DEG=∠BFE=70°,然后利用折叠的性质得∠GEF=∠DEF=70°,然后利用平角的定义可计算出∠AEG的度数;
(2)如图1,先利用互补得到∠EFC=110°,再根据折叠的性质得∠EFH=∠EFC=110°,所以∠MFH=∠EFH-∠BFE=40°,接着利用互余得到∠HMF=50°,然后根据对顶角相等得到∠BMG的度数;
(3)如图2,利用折叠性质得∠MFN=∠MFH=40°,然后计算∠BFE-∠NFH即可.
解答 解:(1)如图1,∵四边形ABCD为矩形,
∴AD∥BC,
∴∠DEG=∠BFE=70°,
∵矩形ABCD沿EF折叠后,点C、D分别落在H、G的位置,
∴∠GEF=∠DEF=70°,
∴∠AEG=180°-70°-70°=40°;
故答案为40;
(2)如图1,
∵∠BFE=70°,
∴∠EFC=110°,
∵矩形ABCD沿EF折叠后,点C、D分别落在H、G的位置,
∴∠EFH=∠EFC=110°,∠MHF=∠D=90°,
∴∠MFH=∠EFH-∠BFE=110°-70°=40°,
∴∠HMF=90°-40°=50°,
∴∠BMG=∠HMF=50°;
(3)如图2,
∵△HMN沿BC折叠得到△MNF,
∴∠MFN=∠MFH=40°,
∴∠EFN=∠BFE-∠NFH=70°-40°=30°.
点评 本题考查了平行线性质::两直线平行,同位角相等;两直线平行,同旁内角互补;两直线平行,内错角相等.也考查了折叠的性质.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
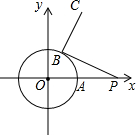 在平面直角坐标系中,以原点O为圆心的圆过点A(2,0),B点为⊙O上任意一点,P(5,0),连接BP,将线段BP绕B点逆时针旋转90°至线段BC,当B点从A点出发,绕圆旋转一周的过程中,C点运动路径长为( )
在平面直角坐标系中,以原点O为圆心的圆过点A(2,0),B点为⊙O上任意一点,P(5,0),连接BP,将线段BP绕B点逆时针旋转90°至线段BC,当B点从A点出发,绕圆旋转一周的过程中,C点运动路径长为( )| A. | 2$\sqrt{2}$π | B. | 4π | C. | 4$\sqrt{2}$π | D. | 6π |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
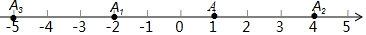 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第2次从点A1向右移动6个单位长度到达点A2,第3次从点A2向左移动9个单位长度到达点A3,…,按照这种移动规律进行下去,第n次移动到达点An,如果点An与原点的距离不小于50,那么n的最小值是33.
如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第2次从点A1向右移动6个单位长度到达点A2,第3次从点A2向左移动9个单位长度到达点A3,…,按照这种移动规律进行下去,第n次移动到达点An,如果点An与原点的距离不小于50,那么n的最小值是33.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.
如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
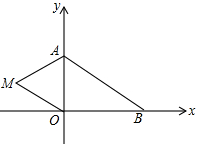 如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a-2|+(b-3)2=0.
如图,在平面直角坐标系中,已知A(0,a),B(b,0),其中a,b满足|a-2|+(b-3)2=0.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
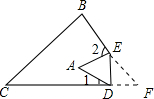 如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部,则∠A与∠1、∠2的关系为( )
如图,把△ABC纸片沿DE折叠,使点A落在四边形BCDE的内部,则∠A与∠1、∠2的关系为( )| A. | ∠A=∠1+∠2 | B. | 3∠A=2(∠1+∠2) | C. | 3∠A=2∠1+∠2 | D. | 2∠A=∠1+∠2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com