
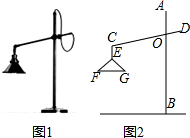
 如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为14cm.
如图1所示的是一种置于桌面上的简易台灯,将其结构简化成图2,灯杆AB与CD交于点O(点O固定),灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,测得OC=20cm,∠COB=70°,∠F=40°,EF=EG,点G到OB的距离为14cm.分析 (1)由EF=EG可知∠G=∠F=40°,由三角形的内角和为180°可求出∠FEG的大小,根据已知条件可得知∠CEF=∠CEG,由∠CEF+∠FEG+∠GEC为周角可得出结论;
(2)延长FG交AB于点N,过点E作EM⊥AB于点M,延长CE交FG于点H,找出四边形CHNM为长方形,在Rt△CMO中由三角函数值求出CM的长度,再结合点G到OB的距离为14cm可求出HG的长度,由△EFG为等腰三角形可得知FG=2HG,从而得出结论.
解答 解:(1)∵EF=EG,∠F=40°,
∴∠G=40°,∠FEG=180°-∠F-∠G=100°,
∵灯罩连杆CE始终保持与AB平行,灯罩下方FG处于水平位置,
∴∠CEG=∠CEF=$\frac{360°-∠FEG}{2}$=130°;
(2)延长FG交AB于点N,过点E作EM⊥AB于点M,延长CE交FG于点H,如图所示.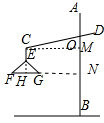
∵CE∥AB,FG处于水平位置,EM⊥AB,
∴四边形CHNM为长方形,CH⊥FG,
∴CM=HN.
在Rt△OMC中,OC=20cm,∠COM=70°,∠OMC=90°,
∴CM=OC•sin∠COM≈20×0.940=18.8(cm),
∵GN=14cm,HN=CM,
∴HG=CM-GN=4.8(cm).
∵EF=EG,CH⊥FG,
∴FH=HG=$\frac{1}{2}$FG,
∴FG=2×4.8=9.6(cm).
答:灯罩的宽度为9.6cm.
点评 本题考查了解直角三角形以及等腰三角形的性质,解题的关键:(1)求出∠FEG的度数;(2)在直角△CMO中求出CM的长度.本题属于中档题,(1)难度不大;(2)稍显复杂,解决该题型题目时,需要借助直角三角形及角的三角函数值来求值.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象交于点C(3,1)
已知:如图,正比例函数y=ax的图象与反比例函数y=$\frac{k}{x}$的图象交于点C(3,1)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
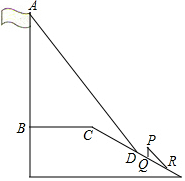 某中学广场上的旗杆AB,在某一时刻它的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为3米,落在斜坡上的影长CD为2米,AB⊥BC,同一时刻,光线与水平面的夹角为60°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(若结果中有根号,请保留根号)
某中学广场上的旗杆AB,在某一时刻它的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为3米,落在斜坡上的影长CD为2米,AB⊥BC,同一时刻,光线与水平面的夹角为60°,1米的竖立标杆PQ在斜坡上的影长QR为2米,求旗杆的高度(若结果中有根号,请保留根号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com