
 已知:抛物线C1:y=x2-2x-3.
已知:抛物线C1:y=x2-2x-3.分析 (1)先把C1的解析式配成顶点式得y=(x-1)2-4,则根据题意可设C2的表达式为y=(x-1)2-4+t,然后把Q点坐标代入求出t即得到抛物线C2的表达式;
(2)设抛物线C1向左平移m(m>0)个单位长度,可使所得的抛物线C3经过坐标原点,则可设顶点式y=(x-1+m)2-4,然后把原点坐标代入即可得到抛物线C3的表达式;
(3)先确定点(1,-4)关于点A(-1,0)对称的对应点的坐标,然后利用顶点式可写出抛物线C4的表达式.
解答 解:(1)y=x2-2x-3=(x-1)2-4,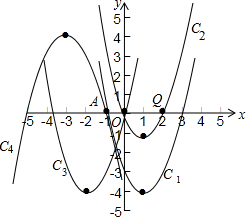
设抛物线C2的表达式为y=(x-1)2-4+t,
把Q(2,0)代入得1-4+t=0,解得t=3,
所以y=(x-1)2-1;
(2)设抛物线C1向左平移m(m>0)个单位长度,可使所得的抛物线C3经过坐标原点,
则C3的表达式为y=(x-1+m)2-4,
把(0,0)代入得(0-1+m)2-4=0,解得m1=-1(舍去),m2=3,
所以C3的表达式为y=(x-1+3)2-4,即y=(x+2)2-4;
(3)点(1,-4)关于点A(-1,0)对称的对应点的坐标为(-3,4),
所以抛物线C4的表达式为y=-(x+3)2+4.
点评 本题考查了二次函数与几何变换:由于抛物线平移后的形状不变,故a不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式.


科目:初中数学 来源: 题型:解答题
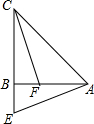 在△ABC中,AB=CB,∠ABC=90°,E为CB延长线上一点,点F在AB上,且AE=CF.
在△ABC中,AB=CB,∠ABC=90°,E为CB延长线上一点,点F在AB上,且AE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
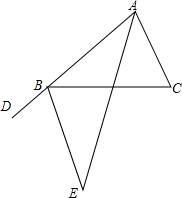 完成下面证明:如图,B是射线AD上一点,AE平分∠DAC,∠DAC=∠C=∠CBE
完成下面证明:如图,B是射线AD上一点,AE平分∠DAC,∠DAC=∠C=∠CBE查看答案和解析>>
科目:初中数学 来源: 题型:解答题
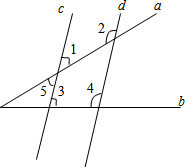 直线c、d分别被直线a、b所截,且∠3+∠4=180°,求证:∠2+∠5=180°.
直线c、d分别被直线a、b所截,且∠3+∠4=180°,求证:∠2+∠5=180°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com