
 如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和B,点M和点N分别是l1 和l2上的动点,MN沿l1和l2平移,⊙O的半径为3,∠1=60°,下列结论错误的是( )
如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和B,点M和点N分别是l1 和l2上的动点,MN沿l1和l2平移,⊙O的半径为3,∠1=60°,下列结论错误的是( )| A. | 若MN与⊙O相切,则AM=3$\sqrt{3}$ | B. | 若∠MON=90°,则MN与⊙O相切 | ||
| C. | MN=4$\sqrt{3}$ | D. | l1和l2的距离为6 |
分析 首先过点N作NC⊥AM于点C,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B,⊙O的半径为1,易求得MN=$\frac{CN}{sin60°}$=4$\sqrt{3}$,l1和l2的距离为6;若∠MON=90°,连接NO并延长交MA于点C,易证得CO=NO,继而可得即O到MN的距离等于半径,可证得MN与⊙O相切;由题意可求得若MN与⊙O相切,则AM=3$\sqrt{3}$或$\sqrt{3}$.
解答 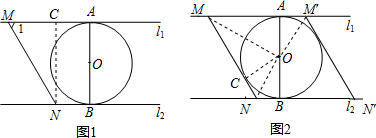 解:如图1,过点N作NC⊥AM于点C,
解:如图1,过点N作NC⊥AM于点C,
∵直线l1∥l2,⊙O与l1和l2分别相切于点A和点B,⊙O的半径为3,
∴CN=AB=6,
∵∠1=60°,
∴MN=$\frac{CN}{sin60°}$=4$\sqrt{3}$,
故C与D正确; 如图3,
如图3,
若∠MON=90°,连接NO并延长交MA于点C,则△AOC≌△BON,
故CO=NO,△MON≌△MOM′,故MN上的高为3,即O到MN的距离等于半径.
故B正确;
如图2,∵MN是切线,⊙O与l1和l2分别相切于点A和点B,
∴∠AMO=$\frac{1}{2}$∠1=30°,
∴AM=3$\sqrt{3}$;
∵∠AM′O=60°,
∴AM′=$\sqrt{3}$,
∴若MN与⊙O相切,则AM=3$\sqrt{3}$或$\sqrt{3}$;
故A错误.
故选A.
点评 此题考查了切线的判定与性质、全等三角形的判定与性质以及三角函数等知识.此题难度较大,注意掌握数形结合思想与分类讨论思想的应用.


 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 支出20元 | B. | 收入20元 | C. | 支出100元 | D. | 收入100元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m-7<n-7 | B. | 3m<3n | C. | -5m>-5n | D. | $\frac{m}{9}$>$\frac{n}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知直线a,b,c,d,c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,则∠2的大小是( )
如图,已知直线a,b,c,d,c⊥a,c⊥b,直线b,c,d交于一点,若∠1=50°,则∠2的大小是( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 用两个相等的实数根 | B. | 有两个不相等的实数根 | ||
| C. | 不确定,与b的取值有关 | D. | 无实数根 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在平行四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于点E,则∠BAE的度数是( )
如图,在平行四边形ABCD中,DB=DC,∠C=70°,AE⊥BD于点E,则∠BAE的度数是( )| A. | 65° | B. | 60° | C. | 55° | D. | 50° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1.354×1012 | B. | 1.354×1011 | C. | 1.354×1010 | D. | 1.354×109 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com