练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图，是某公园的一角，∠AOB=90°，的半径OA长是6米，点C是OA的中点，点D在上，CD∥OB，则图中草坪区（阴影部分）的面积是（　　）

    　

    A．

    （3π+）米

    B．

    （π+）米

    C．

    （3π+9）米

    D．

    （π﹣9）米


    A解：如图，连接OD，∵∠AOB=90°，CD∥OB，

    ∴∠OCD=180°﹣∠AOB=180°﹣90°=90°，

    ∵点C是OA的中点，

    ∴OC=OA=OD=×6=3米，

    ∴∠CDO=30°，

    ∴∠COD=90°﹣30°=60°，

    ∴CD=OC=3，

    ∵CD∥OB，

    ∴∠BOD=∠CDO=30°，

    ∴S阴影=S△COD+S扇形OBD，

    =×3×3+，

    =+3π．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    如图，一次函数y1=k1x+b（k1≠0）的图象与反比例函数y2=k2x+b（k2≠0）的图象交于A，B两点，观察图象，当y1＞y2时，x的取值范围是　　．

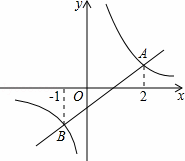
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图是由5个小立方块所搭成的几何体的俯视图，小正方形中的数字表示该位置小立方块的个数，这个几何体的主视图是（　　）

    　

    A．

    B．

    C．

    D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知AB是半圆O的直径，点C是半圆O上的动点，点D是线段AB延长线上的动点，在运动过程中，保持CD=OA．

    （1）当直线CD与半圆O相切时（如图①），求∠ODC的度数；

    （2）当直线CD与半圆O相交时（如图②），设另一交点为E，连接AE，若AE∥OC，

    ①AE与OD的大小有什么关系？为什么？

    ②求∠ODC的度数．

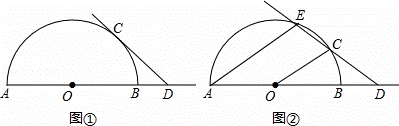
    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在数据1、3、5、5、7中，中位数是（　　）

    　

    A．

    3

    B．

    4

    C．

    5

    D．

    7

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，PA，PB分别切⊙O于点A、B，点C在⊙O上，且∠ACB=50°，则∠P=　　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


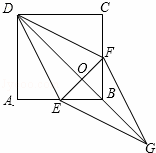
    如图，在正方形ABCD中，点E、F分别在边AB、BC上，∠ADE=∠CDF．

    （1）求证：AE=CF；

    （2）连结DB交CF于点O，延长OB至点G，使OG=OD，连结EG、FG，判断四边形DEGF是否是菱形，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    每年4月23日是“世界读书日”，为了了解某校八年级500名学生对“世界读书日”的知晓情况，从中随机抽取了50名学生进行调查．在这次调查中，样本是（　　）

    　

    A．

    500名学生

    　

    B．

    所抽取的50名学生对“世界读书日”的知晓情况

    　

    C．

    50名学生

    　

    D．

    每一名学生对“世界读书日”的知晓情况

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    查看答案和解析>>

    同步练习册答案