
【题目】已知,在等腰△ABC中,AB=AC,AD⊥BC于点D,以AC为边作等边△ACE,直线BE交直线AD于点F.如图,60°≤∠BAC≤120°,△ACF与△ABC在直线AC的同侧.
(1)①补全图形;
②∠EAF+∠CEF= ;
(2)猜想线段FA,FB,FE的数量关系,并证明你的结论;
(3)若BC=2,则AF的最大值为 .
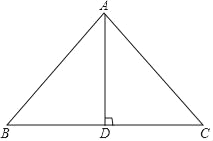
【答案】(1)①图形如图 1 所示;②结论:∠EAF+∠CEF=60°,理由见解析;(2)结论:FA=FE+FB.理由见解析;(3)AF 的最大值为![]() .
.
【解析】
(1)①根据要求画出图形,如图1所示;
②结论:∠EAF+∠CEF=60°如图1中,以A为圆心,AB为半径画圆.作AH⊥BE于H.首先证明∠EBC=∠FAH=30°,根据三角形的内角和定理和外角的性质即可解决问题;
(2)结论:FA=FE+FB.如图2中,在FA上取一点K,使得FK=FE,连接EK.只要证明△AEK≌△CEF(SAS),即可解决问题;
(3)因为60°≤∠BAC≤120°,所以观察图象可知,当∠BAC=60°时,AF的值最大,求出AD,DF即可解决问题;
(1)①图形如图 1 所示;
②结论:∠EAF+∠CEF=60°
理由:如图 1 中,以 A 为圆心,AB 为半径画圆.作 AH⊥BE 于 H.

∵AB=AC=AE,
∴B,E,C 在⊙A 上,
∵△AEC 是等边三角形,
∴∠EAC=60°,
∴∠EBC=![]() EAC=30°,
EAC=30°,
∵AB=AE,AH⊥BE,
∴∠EAH= ![]() ∠BAE,
∠BAE,
∵∠BCE= ![]() ∠BAE,
∠BAE,
∴∠BCE=∠EAH,
∴AD⊥BC,
∴∠BDF=∠AHF=90°,∠BFD=60°,
∴∠HAF=30°,
∴∠EAF+∠CEF=∠EAF+∠EBC+∠BCE=∠EAF+∠EAH+∠EBC=30°+30°=60°.
(2)结论:FA=FE+FB.

理由:如图 2 中,在 FA 上取一点 K,使得 FK=FE,连接 EK.
∵FE=CK,∠EFK=60°,
∴△EFK 是等边三角形,
∴EK=EF,∠EKF=∠KEF=60°,
∵∠AEC=∠KEF=60°,
∴∠AEK=∠CEF,
∵AE=EC,EK=EF,
∴△AEK≌△CEF(SAS),
∴AK=FC,
∵AD 垂直平分线段 BC,
∴FB=CF,
∴FA=FK+AK=FE+FC=FE+FB.
如图 3 中.

∵60°≤∠BAC≤120°,
观察图象可知,当∠BAC=60°时,AF 的值最大, 此时∵AB=AC=BC=2,AF⊥BC,
∴AD=ABsin60°=![]() ,DF=BDtan30°=
,DF=BDtan30°= ![]() ,
,
∴AF=![]() +
+![]() =
=![]() ,
,
∴AF 的最大值为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,CB=CA,∠ACB=90°,点D在边BC上(与B,C不重合),四边形ADEF为正方形,过点F作FG⊥CA,交CA的延长线于点G,连接FB,交DE于点Q,给出以下结论:①AC=FG;②S△FAB∶S四边形CBFG=1∶2;③∠ABC=∠ABF;④AD2=FQ·AC,其中正确结论的个数是( )
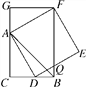
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(4,0),B(0,3),C(4,3),I是△ABC的内心,将△ABC绕原点逆时针旋转90°后,I的对应点I′的坐标为_____.
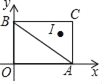
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,半圆O的直径DE=10cm,△ABC中,∠ACB=90°,∠ABC=30°,BC=10cm,半圆O以1cm/s的速度从右到左运动,在运动过程中,D、E点始终在直线BC上,设运动时间为t(s),当t=0(s)时,半圆O在△ABC的右侧,OC=6cm,那么,当t为_____s时,△ABC的一边所在直线与半圆O所在的圆相切.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点B的坐标为(1,0)
(1)在图l中画出△ABC关于x轴对称的△A1B1C1;
(2)在图2中,以点O为位似中心,将△ABC放大,使放大后的△A2B2C2与△ABC的对应边的比为2:1(画出一种即可). 直接写出点A的对应点A2的坐标.
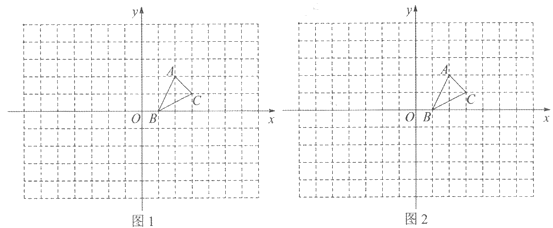
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线y=![]() (x>0)上的一动点,过A作AC⊥y轴,垂足为点C,作AC的垂直平分线交双曲线于点B,交x轴于点D.当点A在双曲线上从左到右运动时,对四边形ABCD的面积的变化情况,小明列举了四种可能:
(x>0)上的一动点,过A作AC⊥y轴,垂足为点C,作AC的垂直平分线交双曲线于点B,交x轴于点D.当点A在双曲线上从左到右运动时,对四边形ABCD的面积的变化情况,小明列举了四种可能:

①逐渐变小;
②由大变小再由小变大;
③由小变大再由大变小;
④不变.
你认为正确的是_____.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() (k≠0)的图象经过点A(﹣2,m),过点A作AB⊥x轴于点B,且△AOB的面积为4.
(k≠0)的图象经过点A(﹣2,m),过点A作AB⊥x轴于点B,且△AOB的面积为4.
(Ⅰ)求k和m的值;
(Ⅱ)设C(x,y)是该反比例函数图象上一点,当1≤x≤4时,求函数值y的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为美化环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
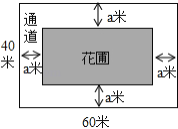
(1)当a=10米时,花圃的面积=
(2)通道的面积与花圃的面积之比能否恰好等于3:5,如果可以,求出此时通道的宽.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y=![]() (k≠0)的图象经过点A(﹣2,m),过点A作AB⊥x轴于点B,且△AOB的面积为4.
(k≠0)的图象经过点A(﹣2,m),过点A作AB⊥x轴于点B,且△AOB的面积为4.
(Ⅰ)求k和m的值;
(Ⅱ)设C(x,y)是该反比例函数图象上一点,当1≤x≤4时,求函数值y的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com