练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．如图，OP平分∠MON，PA⊥ON于点A，点Q是射线OM上一个动点，若PA=8，则PQ的最小值为8．

    分析 过P作PE⊥OM于E，当Q和E重合时，PQ的值最小，根据角平分线性质得出PE=PA，即可求出答案．

    解答 解：
    过P作PE⊥OM于E，当Q和E重合时，PQ的值最小，
    ∵OP平分∠MON，PA⊥ON，PA=8，
    ∴PE=PA=8，
    即PQ的最小值是8，
    故答案为：8．

    点评 本题考查了角平分线性质，垂线段最短的应用，能正确作出辅助线是解此题的关键，注意：角平分线上的点到角的两边的距离相等．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    16．先化简，再求值：（x+2）2-4x（x+1），其中x=-1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．已知一个二次函数y=ax2（a≠0）的图象经过（-2，6），则下列点中不在该函数的图象上的是（　　）
    A．（2，6）B．（1，1.5）C．（-1，1.5）D．（2，8）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    14．如图，在矩形ABCD中，AB=4，AD=3，若以点A为圆心，以4为半径作⊙A，则下列各点在⊙A外的是（　　）
    A．点AB．点BC．点CD．点D

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

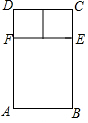    1．如图是一种窗框的设计示意图，矩形ABCD被分成上下两部分，上部的矩形CDFE由两个正方形组成，制作窗框的材料总长为6m．
    （1）若AB为1m，直接写出此时窗户的透光面积$\frac{5}{4}$m2；   
    （2）设AB=x，求窗户透光面积S关于x的函数表达式，并求出S的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    11．-2016的绝对值是2016；-2016的相反数是2016；-$\frac{1}{2016}$的倒数是-2016．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

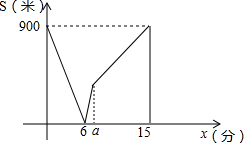    18．甲、乙两人在笔直的路上匀速行走，甲从A地步行前往B地，乙从B地步行前往A地，甲、乙两人同时出发，甲先到达B地后原地休息，甲、乙两人之间的距离S（米）与乙步行的时间t（分）之间的函数关系的图象如图所示，则a=10分钟．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

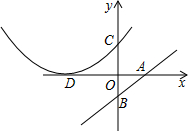    15．如图，直线AB的函数表达式为y=$\frac{m}{4}$x-m（m≠0，m为常数），点A、B分别在x轴、y轴上，tan∠OAB=$\frac{3}{4}$，点B关于x轴的对称点为点C，以D（-6，0）为顶点的抛物线经过点C．
    （1）求抛物线的解析式；
    （2）在x轴上有点P，以点的C，O，P为顶点的△COP与△ABO相似，请求出点P的坐标；
    （3）动点Q在抛物线上，当点Q到直线AB的距离最小时，求出点Q的坐标及最小距离．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

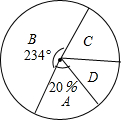    16．某中学为了科学建设“学生健康成长工程”，随机抽取了部分学生家庭对其家长进行了主题“周末孩子在家您关心了吗？”的调查问卷，将收回的调查问卷进行了分析整理，得到了如下的样本统计图表和扇形统计图：
    代号情况分类家庭数
    A带孩子玩且关心其作业完成情况8
    B只关心其作业完成情况m
    C只带孩子玩4
    D既不带孩子玩也不关心其作业完成情况n
    （1）求m，n的值；
    （2）该校学生家庭总数为500，学校决定按比例在B、C、D类家庭中抽取家长组成培训班，其比例为B类20%，C、D类各取60%，请你估计该培训班的家庭数；
    （3）若在C类家庭中只有一个是城镇家庭，其余是农村家庭，请用列举法求出C类中随机抽出2个家庭进行深度家访，其中有一个是城镇家庭的概率．

    查看答案和解析>>

    同步练习册答案