
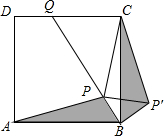
 如图,点P是正方形ABCD内一点,点P到点A,B和C的距离分别为$\sqrt{10}$,1,2$\sqrt{2}$,△ABP绕点B旋转至△CBP′,连结PP′,并延长BP与DC相交于点Q,则∠CPQ的大小为45(度)
如图,点P是正方形ABCD内一点,点P到点A,B和C的距离分别为$\sqrt{10}$,1,2$\sqrt{2}$,△ABP绕点B旋转至△CBP′,连结PP′,并延长BP与DC相交于点Q,则∠CPQ的大小为45(度) 分析 由旋转性质可得△APB≌△CP′B,则有PB=P′B=1、∠PBA=∠P′BC、PA=P′C=$\sqrt{10}$,继而可得∠P′BC+∠PBC=90°、∠BPP′=45°、PP′=$\sqrt{2}$,再根据勾股定理逆定理可得△PCP′为直角三角形且∠CPP′=90°,即可得答案.
解答 解:由旋转性质可得△APB≌△CP′B,
∴PB=P′B=1,∠PBA=∠P′BC,PA=P′C=$\sqrt{10}$,
又∵四边形ABCD是正方形,
∴∠PBA+∠PBC=90°,
∴∠P′BC+∠PBC=90°,即∠PBP′=90°,
∴△PBP′为等腰直角三角形,
∴∠BPP′=45°,PP′=$\sqrt{P{B}^{2}+P′{B}^{2}}$=$\sqrt{2}$,
∵PP′2+PC2=2+8=10=P′C2,
∴△PCP′为直角三角形,且∠CPP′=90°,
∴∠CPQ=180°-∠BPP′-∠CPP′=45°,
故答案为:45.
点评 本题主要考查旋转的性质与正方形的性质,根据旋转变换对应边相等、对应角相等及勾股定理逆定理得出两直角三角形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一游客在某城市旅游期间,沿街步行前往著名的电视塔观光,他在A处望塔顶C的仰角为30°,继续前行250m后到达B处,此时望塔顶的仰角为45°.已知这位游客的眼睛到地面的距离约为170cm,假若游客所走路线直达电视塔底.请你计算这座电视塔大约有多高?(结果保留整数.$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4;E,F分别是两次测量时游客眼睛所在的位置.)
如图,一游客在某城市旅游期间,沿街步行前往著名的电视塔观光,他在A处望塔顶C的仰角为30°,继续前行250m后到达B处,此时望塔顶的仰角为45°.已知这位游客的眼睛到地面的距离约为170cm,假若游客所走路线直达电视塔底.请你计算这座电视塔大约有多高?(结果保留整数.$\sqrt{3}$≈1.7,$\sqrt{2}$≈1.4;E,F分别是两次测量时游客眼睛所在的位置.)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$ | B. | $\sqrt{\frac{1}{2}}$ | C. | $\sqrt{12}$ | D. | $\sqrt{0.2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,四边形ABCD中,AB∥CD,AD∥BC,∠B=90°.
如图,四边形ABCD中,AB∥CD,AD∥BC,∠B=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com