
【题目】如图1,某容器由A、B、C三个长方体组成,其中A、B、C的底面积分别为25cm2、10cm2、5cm2,C的容积是容器容积的![]() (容器各面的厚度忽略不计).现以速度v(单位:cm3/s)均匀地向容器注水,直至注满为止.图2是注水全过程中容器的水面高度h(单位:cm)与注水时间t(单位:s)的函数图象.
(容器各面的厚度忽略不计).现以速度v(单位:cm3/s)均匀地向容器注水,直至注满为止.图2是注水全过程中容器的水面高度h(单位:cm)与注水时间t(单位:s)的函数图象.
⑴在注水过程中,注满A所用时间为______s,再注满B又用了_____s;
⑵求A的高度hA及注水的速度v;
⑶求注满容器所需时间及容器的高度.

【答案】(1)10s,8s(2)A的高度hA为4 cm,注水速度v为10 cm3/s(3)注满这个容器所需时间24 s,容器的高度为24 cm
【解析】分析:(1)看函数图象可得答案;
(2)根据函数图象所给时间和高度列出一个含有hA及v的二元一次方程组,解此方程组可得答案;
(3)根据C的容积和总容积的关系求出C的容积,再求C的高度及注满C的时间,就可以求出注满容器所需时间及容器的高度.
详解:(1)看函数图象可知,注满A所用时间为10s,再注满B又用了 8s;
(2)根据题意和函数图象得,
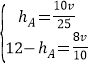 ,
,
解得![]() ;
;
答:A的高度hA是4cm,注水的速度v是10cm3/s;
(3)设C的容积为ycm3,则有,
4y=10v+8v+y,将v=10代入计算得y=60,
那么容器C的高度为:60÷5=12(cm),
故这个容器的高度是:12+12=24(cm),
∵B的注水时间为8s,底面积为10cm2,v=10cm3/s,
∴B的高度=8×10÷10=8(cm),
注满C的时间是:60÷v=60÷10=6(s),
故注满这个容器的时间为:10+8+6=24(s).
答:注满容器所需时间为24s,容器的高度为24cm.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b﹣1)x+c的图象可能是( ) 
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
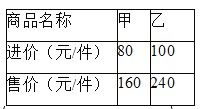
【题目】某商场同时购进甲、乙两种商品共![]() 件,其进价和售价如右表,设其中甲种商品购进
件,其进价和售价如右表,设其中甲种商品购进![]() 件.
件.
(1)直接写出购进乙种商品的件数;(用含![]() 的代数式表示)
的代数式表示)
(2)若设该商场售完这![]() 件商品的总利润为
件商品的总利润为![]() 元.
元.
①求![]() 与
与![]() 的函数关系式;
的函数关系式;
②该商品计划最多投入![]() 元用于购买这两种商品,则至少要购进多少件甲商品?若售完这些商品,则商场可获得的最大利润是多少元?
元用于购买这两种商品,则至少要购进多少件甲商品?若售完这些商品,则商场可获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节约意识,我市出台阶梯电价计算方案如下表:
价目表 | |
不超过 |
|
超过 |
|
超过 |
|
注:电费按月结算 | |
![]() 某户居民
某户居民![]() 月份应缴电费
月份应缴电费![]() 元,该户居民
元,该户居民![]() 月份用电多少度?
月份用电多少度?
![]() 某户居民
某户居民![]() 月份用电
月份用电![]() 度,应缴电费
度,应缴电费![]() 元,求
元,求![]() 的值;
的值;
![]() 用
用![]() (度)表示月用电量,请根据
(度)表示月用电量,请根据![]() 的不同取值范围用含
的不同取值范围用含![]() 的代数式表示该月应缴电费.
的代数式表示该月应缴电费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的材料
勾股定理神秘而美妙,它的证法多种多样,下面是教材中介绍的一种拼图证明勾股定理的方法.

先做四个全等的直角三角形,设它们的两条直角边分别为a,b,斜边为c,然后按图1的方法将它们摆成正方形.
由图1可以得到![]() ,
,
整理,得![]() .
.
所以![]() .
.
如果把图1中的四个全等的直角三角形摆成图2所示的正方形,
请你参照上述证明勾股定理的方法,完成下面的填空:
由图2可以得到 ,
整理,得 ,
所以 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年9月28日-12月31日,山东临沂灯展中千万盏彩灯点亮300亩天然花海.某日,从晚上17时开始每小时进入灯展的人数约为900人(之前该灯展有游客400人),同时每小时走出灯展的人数约为600人,已知该灯展的饱和人数约为1600人,则该灯展人数饱和时的时间约为( )
A. 21时 B. 22时 C. 23时 D. 24时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】给出如下结论:①单项式﹣![]() 的系数为﹣
的系数为﹣![]() ,次数为2;②当x=5,y=4时,代数式x2﹣y2的值为1;③化简(x+
,次数为2;②当x=5,y=4时,代数式x2﹣y2的值为1;③化简(x+![]() )﹣2(x﹣
)﹣2(x﹣![]() )的结果是﹣x+
)的结果是﹣x+![]() ;④若单项式
;④若单项式![]() ax2yn+1与﹣
ax2yn+1与﹣![]() axmy4的和仍是单项式,则m+n=5.其中正确的结论是_____(填序号)
axmy4的和仍是单项式,则m+n=5.其中正确的结论是_____(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图的![]() 方阵图中,处于同一横行、同一竖列、同一斜对角线上的
方阵图中,处于同一横行、同一竖列、同一斜对角线上的![]() 个数之和都相等.现在方阵图中已填写了一些数和代数式(其中每个代数式都表示一个数),则
个数之和都相等.现在方阵图中已填写了一些数和代数式(其中每个代数式都表示一个数),则![]() 的值为________,
的值为________,![]() 的值为________,空白处应填写的
的值为________,空白处应填写的![]() 个数的和为________.
个数的和为________.
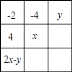
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)![]()
(2)![]()
(3)![]()
(4)[ 2![]() - (
- (![]() )×24 ]÷5×(- 1)2001
)×24 ]÷5×(- 1)2001
(5)![]()
(6) -22 -(-1)2001×(![]() -
- ![]() )÷
)÷![]() +(-3)2
+(-3)2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com