
 如图,Rt△ABC中,∠C=90°,⊙O内切于Rt△ABC,AC边切⊙O于点D,若AC=4,BC=3,则tan∠CAO的值为( )
如图,Rt△ABC中,∠C=90°,⊙O内切于Rt△ABC,AC边切⊙O于点D,若AC=4,BC=3,则tan∠CAO的值为( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
| OD |
| AD |
| 1 |
| 3 |
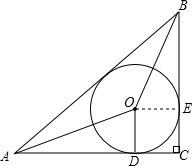 解:设BC切⊙O于点E,连接OE,设⊙O的半径是r,
解:设BC切⊙O于点E,连接OE,设⊙O的半径是r,| AC2+BC2 |
| 3+4-5 |
| 2 |
| OD |
| AD |
| 1 |
| 3 |


科目:初中数学 来源: 题型:
 如图是步枪在瞄准时的示意图,从眼睛到准星的距离OE为80cm,步枪上的准星宽度AB为0.2cm,目标的正面宽度CD为50cm,则眼睛到目标的距离OF是( )
如图是步枪在瞄准时的示意图,从眼睛到准星的距离OE为80cm,步枪上的准星宽度AB为0.2cm,目标的正面宽度CD为50cm,则眼睛到目标的距离OF是( )| A、20000m |
| B、400m |
| C、200m |
| D、199.2m |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,为某食品厂根据通风需要设置的四边形通风调节装置,AB、CD为铁条(宽度不计),O为AB的三等分点、CD的中点,AB=3米,CD=2米,AB可绕O点旋转,阴影部分为遮挡幔布(不通风),空白处可通风,则最大通风面积为( )
如图,为某食品厂根据通风需要设置的四边形通风调节装置,AB、CD为铁条(宽度不计),O为AB的三等分点、CD的中点,AB=3米,CD=2米,AB可绕O点旋转,阴影部分为遮挡幔布(不通风),空白处可通风,则最大通风面积为( )| A、6m2 |
| B、3m2 |
| C、1.5m2 |
| D、无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com