
分析 (1)去括号、移项、合并同类项,系数化成1即可求解;
(2)去分母,去括号、移项、合并同类项,系数化成1即可求解.
解答 解:(1)去括号,得:3x+6-8≥1-2x+2,
移项,得3x+2x≥1+2-6+8,
合并同类项,得5x≥5,
系数化成1得:x≥1, ;
;
(2)去分母,得3(x-3)-6>2(x-5),
去括号,得3x-9-6>2x-10,
移项,得3x-2x>-10+9+6,
合并同类项,得x>5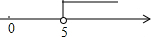 .
.
点评 本题考查了解简单不等式的能力,解答这类题学生往往在解题时不注意移项要改变符号这一点而出错.
解不等式要依据不等式的基本性质:
(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;
(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.


 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在如图所示的平面直角坐标系中,直线y=-x+8与x轴、y轴分别交于A、E两点,点B在线段AE上,且AB=6$\sqrt{2}$.
在如图所示的平面直角坐标系中,直线y=-x+8与x轴、y轴分别交于A、E两点,点B在线段AE上,且AB=6$\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,菱形ABCD中,O是对角线AC、BD的交点,DE⊥AB,E是垂足,DE=3,EB=1,则tan∠AOE=( )
如图,菱形ABCD中,O是对角线AC、BD的交点,DE⊥AB,E是垂足,DE=3,EB=1,则tan∠AOE=( )| A. | $\frac{3}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com