
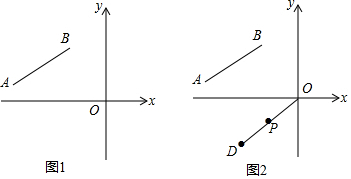
分析 (1)利用非负性即可确定出a,b;
(2)先确定出点A,B的坐标,进而得出直线AB解析式,即可得出点E的坐标,再用三角形的面积公式建立方程求解即可;
(3)先确定出OD的解析式,将点P的坐标代入化简即可得出结论.
解答 解:(1)∵$\sqrt{a+5}$+$\sqrt{b-3}$=0.
∴a+5=0,b-3=0,
∴a=-5,b=3,
故答案:-5,3;
(2)存在,理由:如图1,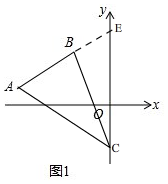
延长AB交y轴于E,
设C(0,c),
∵a=-5,b=3,
∴A(-5,1),B(-2,3),
∴AB的解析式为y=$\frac{2}{3}$x+$\frac{10}{3}$(-5≤x≤-2),
∴E(0,$\frac{10}{3}$),
∴CE=|c-$\frac{10}{3}$|,
∵S△ABC=8,
∴S△ABC=S△ACE-S△BCE=$\frac{1}{2}$CE•|xA|-$\frac{1}{2}$CE•|xB|=$\frac{1}{2}$CE•(|xA|-|xB|)=$\frac{1}{2}$×|c-$\frac{10}{3}$|×(5-2)=8,
∴|c-$\frac{8}{3}$|=$\frac{16}{3}$,
∴c=$\frac{24}{3}$或c=-$\frac{8}{3}$,
∴C(0,$\frac{24}{3}$)或(0,-$\frac{8}{3}$);
(3)∵将线段BA平移得到线段OD,
∴OD的解析式为y=$\frac{2}{3}$x(-3≤x≤0),
∵点P(m,n)在线段OD上,
∴n=$\frac{2}{3}$m,
∴3n-2n=0.
点评 此题是几何变换综合题,主要考查了非负性,待定系数法,三角形的面积公式,解(1)的关键是掌握非负性,解(2)的关键是用三角形的面积公式建立方程,解(3)的关键是求出OD的解析式.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{4}=±2$ | B. | $2\sqrt{3}=\sqrt{6}$ | C. | $2+\sqrt{3}=3\sqrt{3}$ | D. | $\sqrt{8}-\sqrt{2}=\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10个 | B. | 15个 | C. | 18个 | D. | 30个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
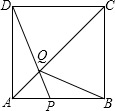 如图,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连结DP交AC于点Q.
如图,在边长为4的正方形ABCD中,点P在AB上从A向B运动,连结DP交AC于点Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com