
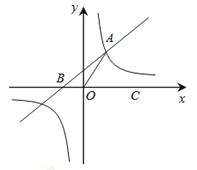
【题目】如图,在平面直角坐标系中,一次函数 y=nx+2(n≠0)的图像与反比例函数 y ![]() (m≠0)在第一象限内的图像交于点 A,与 x 轴交于点 B,线段 OA=5,C 为 x 轴正半轴上一点,且 sin AOC
(m≠0)在第一象限内的图像交于点 A,与 x 轴交于点 B,线段 OA=5,C 为 x 轴正半轴上一点,且 sin AOC ![]() .
.
(1)求一次函数和反比例函数的解析式;
(2)求△ AOB 的面积;
(3)请直接写出不等式 nx 2 ![]() 的解.
的解.
【答案】(1)y=![]() x+2(2)6(3)x<﹣6或0<x<3
x+2(2)6(3)x<﹣6或0<x<3
【解析】
(1)过A点作AD⊥x轴于点D,根据已知的∠AOC的正弦值以及OA的长,利用三角形函数的定义求出AD的长,再利用勾股定理求出OD的长,即可得到点A的坐标,把点A的坐标分别代入到反比例函数和一次函数的解析式中即可确定出两函数的解析式;
(2)根据x轴上点的特征,令一次函数的y=0,求出x的值,确定出点B的坐标,得到线段OB的长,利用三角形的面积公式即可求出三角形AOB的面积;
(3)根据图示可知,不等式nx≤![]() ﹣2的解集.
﹣2的解集.
(1)过A点作AD⊥x轴于点D.
∵sin∠AOC=![]() =
=![]() ,OA=5,∴AD=4.在Rt△AOD中,由勾股定理得:DO=3.
,OA=5,∴AD=4.在Rt△AOD中,由勾股定理得:DO=3.
∵点A在第一象限,∴点A的坐标为(3,4),将A的坐标为(3,4)代入y=![]() ,得m=3×4=12,∴该反比例函数的解析式为y=
,得m=3×4=12,∴该反比例函数的解析式为y=![]() ,将A的坐标为(3,4)代入y=nx+2得:n=
,将A的坐标为(3,4)代入y=nx+2得:n=![]() ,∴一次函数的解析式是y=
,∴一次函数的解析式是y=![]() x+2;
x+2;
(2)在y=![]() x+2中,令y=0,则x=﹣3,∴点B的坐标是(﹣3,0),∴OB=3,又AD=4,∴S△AOB=
x+2中,令y=0,则x=﹣3,∴点B的坐标是(﹣3,0),∴OB=3,又AD=4,∴S△AOB=![]() OBAD=
OBAD=![]() ×3×4=6,∴△AOB的面积为6;
×3×4=6,∴△AOB的面积为6;
(3)依题意,得: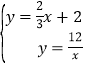 ,解得:
,解得:![]() 或
或![]() ,所以A(3,4),B(﹣6,﹣2),根据图示知,当x<﹣6或0<x<3时,nx≤
,所以A(3,4),B(﹣6,﹣2),根据图示知,当x<﹣6或0<x<3时,nx≤![]() ﹣2.
﹣2.
故nx≤![]() ﹣2的解集是:x<﹣6或0<x<3.
﹣2的解集是:x<﹣6或0<x<3.


科目:初中数学 来源: 题型:
【题目】为了庆祝新年的到来,我市某中学举行“青春飞扬”元旦汇演,正式表演前,把各班的节目分为A(戏类),B(小品类),C(歌舞类),D(其他)四个类别,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.请你根据统计图解答下列问题.
(1)参加汇演的节目数共有 个,在扇形统计图中,表示“B类”的扇形的圆心角为 度,图中m的值为 ;
(2)补全条形统计图;
(3)学校决定从本次汇演的D类节目中,选出2个去参加市中学生文艺汇演.已知D类节目中有相声节目2个,魔术节目1个,朗诵节目1个,请求出所选2个节目恰好是一个相声和一个魔术概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为表彰在某活动中表现积极的同学,老师决定购买文具盒与钢笔作为奖品.已知5个文具盒、2支钢笔共需100元;3个文具盒、1支钢笔共需57元.
(1)每个文具盒、每支钢笔各多少元?
(2)若本次表彰活动,老师决定购买10件作为奖品,若购买![]() 个文具盒,10件奖品共需
个文具盒,10件奖品共需![]() 元,求
元,求![]() 与
与![]() 的函数关系式.如果至少需要购买3个文具盒,本次活动老师最多需要花多少钱?
的函数关系式.如果至少需要购买3个文具盒,本次活动老师最多需要花多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC中,AB=AC=10,BC=16,点F是边BC上不与点B,C重合的一个动点,直线DE垂直平分BF,垂足为D.当△ACF是直角三角形时,线段BD的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
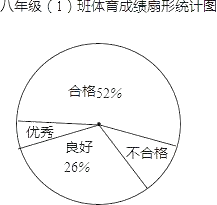
【题目】某校对九年级(1)班全体学生进行体育测试,测试成绩分为优秀、良好、合格和不合格四个等级,根据测试成绩绘制的不完整统计图表如下:
九年级(1)班体育成绩频数分布表:
等级 | 分值 | 频数 |
优秀 | 90﹣100分 | |
良好 | 75﹣89分 | 13 |
合格 | 60﹣74分 | |
不合格 | 0﹣59分 | 9 |
根据统计图表给出的信息,解答下列问题:
(1)九年级(1)班共有多少名学生?
(2)体育成绩为优秀的频数是 ,合格的频数为 ;
(3)若对该班体育成绩达到优秀程度的3个男生和2个女生中随机抽取2人参加学校体育竞赛,恰好抽到1个男生和1个女生的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BC为Rt△ABC的斜边,∠CBA=30°,△ABD,△ACF,△BCE均为正三角形,四边形MNPE是长方形,点F在MN上,点D在NP上,若AC=2,则图中空白部分的面积是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CE⊥AB,BD⊥AC,垂足分别为E、D,BD、CE交于点O,AB=AC,∠B=20°,则∠AOD=( )

A. 20°B. 40°C. 50°D. 55°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com