
若﹣7xm+2y4z2与﹣3x3ynzt是同类项,则m=_____.
1 【解析】试题解析:∵﹣7xm+2y4z2与﹣3x3ynzt是同类项, ∴m+2=3 ∴m=1 故答案为:1. 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:云南省楚雄州2017-2018学年上学期期末教学质量监测九年级数学试卷 题型:单选题
如图,P(x,y)是反比例函数 的图象在第一象限分支上的一个动点,PA⊥x轴于点A,PB⊥y轴于点B,随着自变量x的增大,矩形OAPB的面积( )
的图象在第一象限分支上的一个动点,PA⊥x轴于点A,PB⊥y轴于点B,随着自变量x的增大,矩形OAPB的面积( )
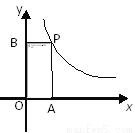
A. 增大 B. 减小 C. 不变 D. 无法确定
C 【解析】试题解析:依题意有矩形OAPB的面积=2×|k|=3,所以随着x的逐渐增大,矩形OAPB的面积将不变. 故选C.查看答案和解析>>
科目:初中数学 来源:人教版九年级年级数学下册第二十九章 达标检测卷 题型:解答题
按规定尺寸作出下面图形的三视图.
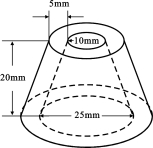
查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省哈尔滨市双城区七年级(上)期末数学试卷(五四学制) 题型:解答题
如图,已知线段AB和CD的公共部分为BD,且BD=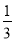 AB=
AB=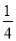 CD,线段AB、CD的中点E、F之间距离是20,求AB、CD的长.
CD,线段AB、CD的中点E、F之间距离是20,求AB、CD的长.
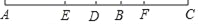
查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省哈尔滨市双城区七年级(上)期末数学试卷(五四学制) 题型:填空题
观察下面一组式子:(1)1×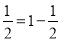 ; (2)
; (2)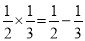 ;(3)
;(3)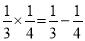 ;(4
;(4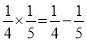 )…
)…
写出这组式子中的第(n)组式子是_____________________.
【解析】试题分析:如果把1看成,那么第一个分数的分母分别为1,2,3,4,…,则第n个数的分母为n,第二个分数的分母分别为2,3,4,…,则第n个数的分母为n+1,分子都是1,所以这组式子中的第n组式子是.故答案为.查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省哈尔滨市双城区七年级(上)期末数学试卷(五四学制) 题型:单选题
为确保信息安全,信息需要加密传输,发送方由明文→密文(解密).接收方由密文→明文(解密)。已知加密规则为:明文a,b,c对应的密文a+1,2b+4,3c+9,例如明文1,2,3对应的密文2,8,18。如果接收方收到密文7,18,15,则解密得到的明文为( )
A. 4,5,6 B. 6,7,2 C. 2,6,7 D. 7,2,6
B 【解析】试题分析:首先根据必须理解密文的加密方法,然后进行计算.根据题意得:a+1=7,2b+4=18,3c+9=15 则a=6,b=7,c=2,即明文为6,7,2.查看答案和解析>>
科目:初中数学 来源:2017-2018学年黑龙江省哈尔滨市双城区七年级(上)期末数学试卷(五四学制) 题型:单选题
有理数6的相反数是( )
A. ﹣6 B. 6 C. 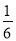 D. ﹣
D. ﹣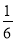
查看答案和解析>>
科目:初中数学 来源:人教版七年级下册数学第五章相交线与平行线单元检测卷 题型:单选题
如图所示,∠1=70°,有下列结论:①若∠2=70°,则AB∥CD;②若∠5=70°,则AB∥CD;③若∠3=110°,则AB∥CD;④若∠4=110°,则AB∥CD.其中正确的有( )
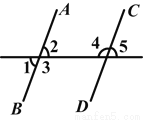
A. 1个 B. 2个 C. 3个 D. 4个
B 【解析】②,④正确.②中∠5=70°,又∠2=∠1=70°(对顶角相等),所以∠5=∠2,所以AB∥CD(同位角相等,两直线平行);④中∠4=110°,又∠2=∠1=70°(对顶角相等),所以∠2+∠4=70°+110°=180°,所以AB∥CD(同旁内角互补,两直线平行).查看答案和解析>>
科目:初中数学 来源:2017-2018学年八年级数学人教版上册 全册综合测试卷 题型:填空题
如图,△ABC是等边三角形,AE=CD,AD、BE相交于点P,BQ⊥DA于Q,PQ=3,EP=1,则DA的长是________.
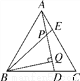
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com