练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
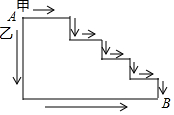
    11．如图，两只蚂蚁以相同的速度沿两条不同的路径，同时从A出发爬到B，则（　　）
    A．乙比甲先到B．甲比乙先到C．甲和乙同时到D．无法确定

    分析 根据平移可得出两蚂蚁行程相同，结合二者速度相同即可得出结论．

    解答 解：∵甲、乙两只蚂蚁的行程相同，且两只蚂蚁的速度相同，
    ∴两只蚂蚁同时到达．
    故选C．

    点评 本题考查了生活中的平移现象，结合图形找出甲、乙两只蚂蚁的行程相等是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    1．下列计算中，正确的是（　　）
    A．a2•a4=a8B．（a3）2=a5C．（3ax）2=9a2x2D．a2+a2=a4

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．计算
    （1）-2+6÷（-2）×$\frac{1}{2}$                
    （2）24-|-0.5|+（-3.2）-|-2$\frac{2}{5}$|-（-4.7）
    （3）-23-|-3|+4÷（-$\frac{3}{8}$）×（-3）
    （4）-0.252+（-0.5）3÷（$\frac{1}{8}$-$\frac{1}{2}$）×（-1）10．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．单项式-x2y3与4xmyn是同类项，则m=2，n=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

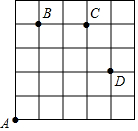    6．如图，一只甲虫在5×5的方格（每小格边长为1）上沿着网格线运动．它从A处出发去看望B、C、D处的其它甲虫，规定：向上向右走均为正，向下向左走均为负．如果从A到B记为：A→B（+1，+4），从B到A记为：B→A（-1，-4），其中第一个数表示左右方向，第二个数表示上下方向．
    （1）图中A→C（+3，+4），B→C（+2，0），C→D（+1，-2）；
    （2）若这只甲虫从A处去甲虫P处的行走路线依次为（+2，+2），（+2，-1），（-2，+3），（-1，-2），请在图中标出P的位置；
    （3）若这只甲虫的行走路线为A→B→C→D，请计算该甲虫走过的路程．
    （4）若图中另有两个格点M、N，且M→A（3-a，b-4），M→N（5-a，b-2），则N→A应记为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．已知方程x2-3x+m=0的一个根是1，则m的值是2，它的另一个根是2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．如图1所示，在直角坐标系中，边长为12的等边△ABC的边BC在x轴上，BC边上的高AD在y轴上，点D与原点O重合，过D点作AB边的垂线，交AB边于点E，交AC的延长线于点M．
    （1）求证：OC=MC；
    （2）将等边△ABC整体沿x轴的正方向匀速平移，当点B到达原点O时，图形停止运动．若边AB与y轴交于点F，请思考并解决以下问题：
    ①如图2，延长CA交y轴于点G．如果△ABC平移的速度为每秒1个单位长度，当△AGF与△CDM全等时，平移了多长时间？
    ②在线段OC上取一点N，连接FN并延长交射线AC于点Q，是否存在一点N，使得CQ=FB？若存在，求线段ON的长；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，已知∠1=∠C，∠2=∠3，那么AD平分∠BAC，请你说明为什么．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．同底数幂的除法公式am÷an=am-n（a≠0，m，n都是正整数，并且m＞n）中，如果m＜n可以得到负整指数幂；a-p=$\frac{1}{{a}^{p}}$（a≠0，p是正整数），即任何不等于0的数的-p次幂等于这个数的p次幂的倒数，请你根据负整指数幂的定义求解下题：
    （$\frac{1}{2}$）-1+|-3|+（2-$\sqrt{3}$）0+（-1）

    查看答案和解析>>

    同步练习册答案