
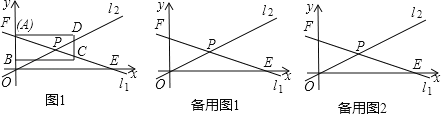
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬µćFµÄ×ų±źĪŖ£Ø0£¬10£©£®µćEµÄ×ų±źĪŖ£Ø20£¬0£©£¬Ö±Ļßl1¾¹żµćFŗĶµćE£¬Ö±Ļßl1ÓėÖ±Ļßl2 ”¢y=![]() xĻą½»ÓŚµćP£®
xĻą½»ÓŚµćP£®
£Ø1£©ĒóÖ±Ļßl1µÄ±ķ“ļŹ½ŗĶµćPµÄ×ų±ź£»
£Ø2£©¾ŲŠĪABCDµÄ±ßABŌŚyÖįµÄÕż°ėÖįÉĻ£¬µćAÓėµćFÖŲŗĻ£¬µćBŌŚĻ߶ĪOFÉĻ£¬±ßADĘ½ŠŠÓŚx Öį£¬ĒŅAB=6£¬AD=9£¬½«¾ŲŠĪABCDŃŲÉäĻßFEµÄ·½ĻņĘ½ŅĘ£¬±ßADŹ¼ÖÕÓėx ÖįĘ½ŠŠ£®ŅŃÖŖ¾ŲŠĪABCDŅŌĆæĆė![]() øöµ„Ī»µÄĖŁ¶ČŌČĖŁŅĘ¶Æ£ØµćAŅĘ¶Æµ½µćEŹ±Ö¹ŅĘ¶Æ£©£¬ÉčŅĘ¶ÆŹ±¼äĪŖtĆė£Øt£¾0£©£®
øöµ„Ī»µÄĖŁ¶ČŌČĖŁŅĘ¶Æ£ØµćAŅĘ¶Æµ½µćEŹ±Ö¹ŅĘ¶Æ£©£¬ÉčŅĘ¶ÆŹ±¼äĪŖtĆė£Øt£¾0£©£®
¢Ł¾ŲŠĪABCDŌŚŅĘ¶Æ¹ż³ĢÖŠ£¬B”¢C”¢DČżµćÖŠÓŠĒŅÖ»ÓŠŅ»øö¶„µćĀäŌŚÖ±Ļßl1»ņl2ÉĻ£¬ĒėÖ±½ÓŠ“³ö“ĖŹ±tµÄÖµ£»
¢ŚČō¾ŲŠĪABCDŌŚŅĘ¶ÆµÄ¹ż³ĢÖŠ£¬Ö±ĻßCD½»Ö±Ļßl1ÓŚµćN£¬½»Ö±Ļßl2ÓŚµćM£®µ±”÷PMNµÄĆ껿µČÓŚ18Ź±£¬ĒėÖ±½ÓŠ“³ö“ĖŹ±tµÄÖµ£®
”¾“š°ø”æ£Ø1£©Ö±Ļßl1µÄ±ķ“ļŹ½ĪŖy=©![]() x+10£¬µćP×ų±źĪŖ£Ø8£¬6£©£»£Ø2£©¢ŁtÖµĪŖ
x+10£¬µćP×ų±źĪŖ£Ø8£¬6£©£»£Ø2£©¢ŁtÖµĪŖ![]() »ņ
»ņ![]() £»¢Śµ±t=
£»¢Śµ±t=![]() Ź±£¬”÷PMNµÄĆ껿µČÓŚ18.
Ź±£¬”÷PMNµÄĆ껿µČÓŚ18.
”¾½āĪö”æ£Ø1£©ĄūÓĆ“ż¶ØĻµŹż·ØĒó½āĪöŹ½£¬ŗÆŹż¹ŲĻµŹ½ĮŖĮ¢·½³ĢĒó½»µć£»
£Ø2£©¢Ł·ÖĪö¾ŲŠĪŌĖ¶Æ¹ęĀÉ£¬ÕŅµ½µćDŗĶµćB·Ö±šŌŚÖ±Ļßl2ÉĻ»ņŌŚÖ±Ļßl1ÉĻŹ±µÄĒéæö£¬ĄūÓĆAD”¢AB·Ö±šæÉŅŌ擳ÉĶ¼Ļóŗį×ų±ź”¢×Ż×ų±źÖ®²ī¹¹Ōģ·½³ĢĒóµćA×ų±ź£¬½ų¶ųĒó³öAF¾ąĄė£»
¢ŚÉčµćA×ų±ź£¬±ķŹ¾”÷PMN¼“æÉ£®
£Ø1£©ÉčÖ±Ļßl1µÄ±ķ“ļŹ½ĪŖy=kx+b£¬
”ßÖ±Ļßl1¹żµćF£Ø0£¬10£©£¬E£Ø20£¬0£©£¬
”ą![]() £¬½āµĆ£ŗ
£¬½āµĆ£ŗ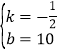 £¬
£¬
Ö±Ļßl1µÄ±ķ“ļŹ½ĪŖy=©![]() x+10£¬
x+10£¬
½ā·½³Ģ×é µĆ
µĆ![]() £¬
£¬
”ąµćP×ų±źĪŖ£Ø8£¬6£©£»
£Ø2£©¢ŁČēĶ¼£¬µ±µćDŌŚÖ±ĻßÉĻl2Ź±£¬

ӧAD=9
”ąµćDÓėµćAµÄŗį×ų±źÖ®²īĪŖ9£¬
”ą½«Ö±Ļßl1ÓėÖ±Ļßl2 µÄ½āĪöŹ½±äŠĪĪŖx=20©2y£¬x=![]() y£¬
y£¬
”ą![]() y©£Ø20©2y£©=9£¬
y©£Ø20©2y£©=9£¬
½āµĆ£ŗy=![]() £¬
£¬
”ąx=20©2y=![]() £¬
£¬
ŌņµćAµÄ×ų±źĪŖ£ŗ£Ø![]() £¬
£¬![]() £©£¬
£©£¬
ŌņAF=![]() £¬
£¬
”ßµćAĖŁ¶ČĪŖĆæĆė![]() øöµ„Ī»£¬
øöµ„Ī»£¬
”ąt=![]() £»
£»
ČēĶ¼£¬µ±µćBŌŚl2 Ö±ĻßÉĻŹ±£¬
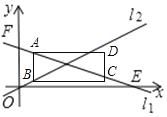
”ßAB=6£¬
”ąµćAµÄׯ×ų±ź±ČµćBµÄׯ×ų±źøß6øöµ„Ī»£¬
”ąÖ±Ļßl1µÄ½āĪöŹ½¼õČ„Ö±Ļßl2 µÄ½āĪöŹ½µĆ£¬
©![]() x+10©
x+10©![]() x=6£¬
x=6£¬
½āµĆx=![]() £¬
£¬
y=©![]() x+10=
x+10=![]() £¬
£¬
ŌņµćA×ų±źĪŖ£Ø![]() £¬
£¬![]() £©
£©
ŌņAF=![]() £¬
£¬
”ßµćAĖŁ¶ČĪŖĆæĆė![]() øöµ„Ī»£¬
øöµ„Ī»£¬
”ąt=![]() £¬
£¬
¹ŹtÖµĪŖ![]() »ņ
»ņ![]() £»
£»
¢ŚČēĶ¼£¬
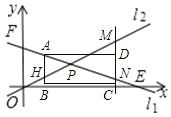
ÉčÖ±ĻßAB½»l2 ÓŚµćH£¬
ÉčµćAŗį×ų±źĪŖa£¬ŌņµćDŗį×ų±źĪŖa+9£¬
ÓÉ¢ŁÖŠ·½·ØæÉÖŖ£ŗMN=![]() £¬
£¬
“ĖŹ±µćPµ½MN¾ąĄėĪŖ£ŗa+9©8=a+1£¬
”ß”÷PMNµÄĆ껿µČÓŚ18£¬
”ą![]() =18£¬
=18£¬
½āµĆ
a1=![]() -1£¬a2=©
-1£¬a2=©![]() -1£ØÉįČ„£©£¬
-1£ØÉįČ„£©£¬
”ąAF=6©![]() £¬
£¬
Ōņ“ĖŹ±tĪŖ![]() £¬
£¬
µ±t=![]() Ź±£¬”÷PMNµÄĆ껿µČÓŚ18.
Ź±£¬”÷PMNµÄĆ껿µČÓŚ18.



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æijŠ£ĪŖĮĖĮĖ½āĮĖ½ā½ŚÄܼõÅÅ”¢Ą¬»ų·ÖĄąµČÖŖŹ¶µÄĘÕ¼°Ēéæö£¬“ÓøĆŠ£2000Ćūѧɜ֊Ė껜³éČ”ĮĖ²æ·Öѧɜ½ųŠŠµ÷²éµ÷²é£¬µ÷²é½į¹ū·ÖĪŖ”°·Ē³£ĮĖ½ā”°”¢”°ĮĖ½ā”±”¢”°ĮĖ½ā½ĻÉŁ”±”¢”°²»ĮĖ½ā”±ĖÄĄą£¬²¢½«µ÷²é½į¹ū»ęÖĘ³öŅŌĻĀĮ½·ł²»ĶźÕūµÄĶ³¼ĘĶ¼£¬Ēėøł¾ŻĶ³¼ĘĶ¼»Ų“šĻĀĮŠĪŹĢā£ŗ
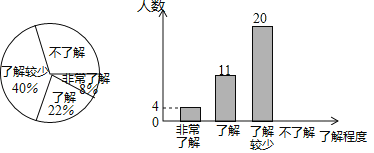
£Ø1£©±¾“Īµ÷²éµÄѧɜ¹²ÓŠ”” ””ČĖ£¬¹Ą¼ĘøĆŠ£2000Ćūѧɜ֊”°²»ĮĖ½ā”±µÄČĖŹżŌ¼ÓŠ”” ””ČĖ£®
£Ø2£©”°·Ē³£ĮĖ½ā”±µÄ4ČĖÖŠÓŠA1£¬A2Į½ĆūÄŠÉś£¬B1£¬B2Į½ĆūÅ®Éś£¬Čō“ÓÖŠĖ껜³éČ”Į½ČĖČ„²Ī¼Ó»·±£ÖŖŹ¶¾ŗČü£¬ĒėÓĆ»Ź÷דĶ¼ŗĶĮŠ±ķµÄ·½·Ø£¬ĒóĒ”ŗĆ³éµ½2ĆūÄŠÉśµÄøÅĀŹ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬µć![]() ŌŚÖ±Ļß
ŌŚÖ±Ļß![]() ÉĻ£¬µć
ÉĻ£¬µć![]() ŌŚÖ±Ļß
ŌŚÖ±Ļß![]() ÉĻ£¬
ÉĻ£¬![]()
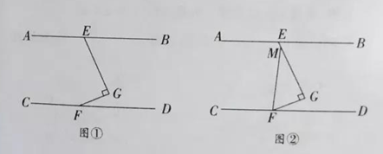
![]() ČēĶ¼¢Ł£¬Čō
ČēĶ¼¢Ł£¬Čō![]() £¬ÅŠ¶Ļ
£¬ÅŠ¶Ļ![]() Óė
Óė![]() µÄĪ»ÖĆ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£»
µÄĪ»ÖĆ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£»
![]() Ķ¼¢Ś£¬ŌŚ
Ķ¼¢Ś£¬ŌŚ![]() µÄ½įĀŪĻĀ£¬
µÄ½įĀŪĻĀ£¬![]() ÉĻÓŠŅ»µć
ÉĻÓŠŅ»µć![]() £¬ĒŅ
£¬ĒŅ![]() £¬ÅŠ¶Ļ
£¬ÅŠ¶Ļ![]() Óė
Óė![]() µÄŹżĮæ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£®
µÄŹżĮæ¹ŲĻµ£¬²¢ĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”抔Ć÷¼ŅŠčŅŖÓĆøÖ¹Ü×ö·ĄµĮ“°£¬°“Éč¼ĘŅŖĒó£¬ĘäÖŠŠčŅŖ³¤ĪŖ 0.8m£¬2.5m ĒŅ“ÖĻøĻąĶ¬µÄøֱֹܷšĪŖ 100 øł£¬32 øł£¬²¢ŅŖĒóÕāŠ©ÓĆĮĻ²»ÄÜŹĒŗø½Ó¶ų³ÉµÄ£®ĻÖøÖ²ÄŹŠ³”µÄÕāÖÖ¹ęøńµÄøÖ¹ÜĆæøłĪŖ 6m£®
£Ø1£©ŹŌĪŹŅ»øł 6m ³¤µÄŌ²øÖ¹ÜÓŠÄÄŠ©²Ć¼ō·½·ØÄŲ£æĒėĢīŠ“ĻĀæÕ£ØÓąĮĻ×÷·Ļ£©£®
·½·Ø¢Ł£ŗµ±Ö»²Ć¼ō³¤ĪŖ 0.8m µÄÓĆĮĻŹ±£¬×ī¶ąæɼō øł£»
·½·Ø¢Ś£ŗµ±ĻČ¼ōĻĀ 1 øł 2.5m µÄÓĆĮĻŹ±£¬ÓąĻĀ²æ·Ö×ī¶ąÄܼō 0.8m ³¤µÄÓĆĮĻ øł£»
·½·Ø¢Ū£ŗµ±ĻČ¼ōĻĀ 2 øł 2.5m µÄÓĆĮĻŹ±£¬ÓąĻĀ²æ·Ö×ī¶ąÄܼō 0.8m ³¤µÄÓĆĮĻ øł£®
£Ø2£©·Ö±šÓĆ£Ø1£©ÖŠµÄ·½·Ø¢ŚŗĶ·½·Ø¢Ūø÷²Ć¼ō¶ąÉŁøł 6m ³¤µÄøֹܣ¬²ÅÄÜøÕŗƵƵ½ĖłŠčŅŖµÄĻąÓ¦ŹżĮæµÄ²ÄĮĻ£æ
£Ø3£©ŹŌĢ½¾æ£ŗ³ż£Ø2£©ÖŠ·½°øĶā£¬ŌŚ£Ø1£©ÖŠ»¹ÓŠÄÄĮ½ÖÖ·½·ØĮŖŗĻ£¬ĖłŠčŅŖ 6m ³¤µÄøÖ¹ÜÓė£Ø2£© ÖŠøłŹżĻąĶ¬£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĮāŠĪABCDÖŠ£¬¶Ō½ĒĻßACÓėBD½»ÓŚµćO£®¹żµćC×÷BDµÄĘ½ŠŠĻߣ¬¹żµćD×÷ACµÄĘ½ŠŠĻߣ¬Į½Ö±ĻßĻą½»ÓŚµćE£®
£Ø1£©ĒóÖ¤£ŗĖıߊĪOCEDŹĒ¾ŲŠĪ£»
£Ø2£©ČōCE=1£¬DE=2£¬ABCDµÄĆ껿ŹĒ”” ””£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
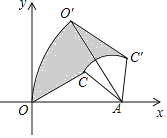
”¾ĢāÄæ”æČēĶ¼£¬”÷OACµÄ¶„µćOŌŚ×ų±źŌµć£¬OA±ßŌŚxÖįÉĻ£¬OA=2£¬AC=1£¬°Ń”÷OACČʵćA°“Ė³Ź±Õė·½ĻņŠż×Ŗµ½”÷O”äAC”䣬Ź¹µĆµćO”äµÄ×ų±źŹĒ£Ø1£¬![]() £©£¬ŌņŌŚŠż×Ŗ¹ż³ĢÖŠĻ߶ĪOCÉعż²æ·Ö£ØŅõÓ°²æ·Ö£©µÄĆ껿ĪŖ______£®
£©£¬ŌņŌŚŠż×Ŗ¹ż³ĢÖŠĻ߶ĪOCÉعż²æ·Ö£ØŅõÓ°²æ·Ö£©µÄĆ껿ĪŖ______£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
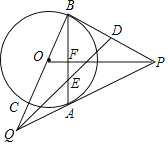
”¾ĢāÄæ”æČēĶ¼£¬PŹĒ”ŃOĶāµÄŅ»µć£¬PA”¢PBŹĒ”ŃOµÄĮ½ĢõĒŠĻߣ¬A”¢BŹĒĒŠµć£¬PO½»ABÓŚµćF£¬ŃÓ³¤BO½»”ŃOÓŚµćC£¬½»PAµÄŃÓ³¤½»ÓŚµćQ£¬Į¬½įAC£®
£Ø1£©ĒóÖ¤£ŗAC”ĪPO£»
£Ø2£©ÉčDĪŖPBµÄÖŠµć£¬QD½»ABÓŚµćE£¬Čō”ŃOµÄ°ė¾¶ĪŖ3£¬CQ=2£¬Ēó![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬¹żµćA£Ø2£¬0£©µÄÖ±Ļß![]() ÓėyÖį½»ÓŚµćB£¬ÓėĖ«ĒśĻß
ÓėyÖį½»ÓŚµćB£¬ÓėĖ«ĒśĻß![]() ½»ÓŚµćP£¬µćPĪ»ÓŚyÖį×ó²ą£¬ĒŅµ½yÖįµÄ¾ąĄėĪŖ1£¬ŅŃÖŖtan”ĻOAB=
½»ÓŚµćP£¬µćPĪ»ÓŚyÖį×ó²ą£¬ĒŅµ½yÖįµÄ¾ąĄėĪŖ1£¬ŅŃÖŖtan”ĻOAB=![]() £®
£®
£Ø1£©·Ö±šĒó³öÖ±ĻßÓėĖ«ĒśĻßĻąÓ¦µÄŗÆŹż±ķ“ļŹ½£»
£Ø2£©¹Ū²ģĶ¼Ļó£¬Ö±½ÓŠ“³ö²»µČŹ½![]() £¾
£¾![]() µÄ½ā¼Æ£®
µÄ½ā¼Æ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
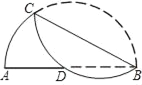
”¾ĢāÄæ”æČēĶ¼£¬ŌŚŅŌABĪŖÖ±¾¶µÄ°ėŌ²ÖŠ£¬½«»”BCŃŲĻŅBCÕŪµž½»ABÓŚµćD£¬ČōAD=5£¬DB=7£®
£Ø1£©ĒóBCµÄ³¤£»
£Ø2£©ĒóŌ²ŠÄµ½BCµÄ¾ąĄė£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com