
【题目】如图,在正方形纸片![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() ,折叠正方形纸片
,折叠正方形纸片![]() ,使
,使![]() 落在
落在![]() 上,点
上,点![]() 恰好与
恰好与![]() 上的点
上的点![]() 重合.展开后,折痕
重合.展开后,折痕![]() 分别交
分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .连接
.连接![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④四边形
;④四边形![]() 是菱形;⑤
是菱形;⑤![]() .
.
其中正确结论的序号是( )
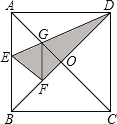
A. ①②③④⑤B. ①②③④C. ①③④⑤D. ①④⑤
【答案】D
【解析】
①根据折叠的性质我们能得出∠ADG=∠ODG,也就求出了∠ADG的度数,那么在三角形AGD中用三角形的内角和即可求出∠AGD的度数;
②根据AE=EF<BE即AE<![]() AB,∴tan∠AED=
AB,∴tan∠AED=![]() >2,
>2,
③根据△AGD与△OGD同高不等底,即可判断;
④根据同位角相等得到EF∥AC,GF∥AB,由折叠的性质得出AE=EF,即可判定四边形AEFG是菱形;
⑤通过相似三角形DEF和DOG得出EF和OG的比例关系,然后再在![]() BEF中求出BE和EF的关系,进而求出BE和OG的关系.
BEF中求出BE和EF的关系,进而求出BE和OG的关系.
解:因为在正方形纸片ABCD中,折叠正方形纸片ABCD,使AD落在BD上,点A恰好与BD上的点F重合,所以∠GAD=45°,∠ADG=![]() ∠ADO=22.5°,
∠ADO=22.5°,
所以∠AGD=112.5°,所以①正确.
因为tan∠AED=![]() ,因为AE=EF<BE,
,因为AE=EF<BE,
所以AE<![]() AB,所以tan∠AED=
AB,所以tan∠AED=![]() >2,因此②错.
>2,因此②错.
因为AG=FG>OG,△AGD与△OGD同高,
所以S△AGD>S△OGD,所以③错.
根据题意可得:AE=EF,AG=FG,又因为EF∥AC,
所以∠FEG=∠AGE,又因为∠AEG=∠FEG,
所以∠AEG=∠AGE,所以AE=AG=EF=FG,
所以四边形AEFG是菱形,因此④正确.
由折叠的性质设BF=EF=AE=1,则AB=1+![]() ,BD=2+
,BD=2+![]() ,DF=1+
,DF=1+![]() ,由此可求
,由此可求![]() =
=![]() ,
,
∵∠DFE=∠BAD=∠AOD=90°(折叠的性质),
∵四边形AEFG是菱形,
∴EF∥AG∥AC,
∴△DOG∽△DFE,
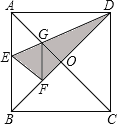
∴![]() =
=![]() =
=![]()
![]() EF=2OG,
EF=2OG,
在直角三角形BEF中,∠EBF=45°,
所以△BEF是等腰直角三角形,同理可证△OFG是等腰直角三角形,
在等腰直角三角形BEF和等腰直角三角形OFG中,BE2=2EF2=2GF2=2×2OG2,
所以BE=2OG.因此⑤正确.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是![]()
![]()
A. 某种彩票的中奖机会是![]() 则买100张这种彩票一定会中奖
则买100张这种彩票一定会中奖
B. 为了解全国中学生的睡眠情况,应该采用普查的方式
C. 一组数据3,4,5,5,5,6,10的平均数大于中位数
D. 同时抛掷两枚均匀的硬币,出现一枚正面朝上且另一枚反面朝上的概率是![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】元旦期间,某超市销售两种不同品牌的苹果,已知1千克甲种苹果和1千克乙种苹果的进价之和为18元.当销售1千克甲种苹果和1千克乙种苹果利润分别为4元和2元时,陈老师购买3千克甲种苹果和4千克乙种苹果共用82元.
(1)求甲、乙两种苹果的进价分别是每千克多少元?
(2)在(1)的情况下,超市平均每天可售出甲种苹果100千克和乙种苹果140千克,若将这两种苹果的售价各提高1元,则超市每天这两种苹果均少售出10千克,超市决定把这两种苹果的售价提高x元,在不考虑其他因素的条件下,使超市销售这两种苹果共获利960元,求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
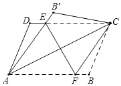
【题目】如图,现将平行四边形ABCD沿其对角线AC折叠,使点B落在点B′处.AB′与CD交于点E.
(1)求证:△AED≌△CEB′;
(2)过点E作EF⊥AC交AB于点F,连接CF,判断四边形AECF的形状并给予证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
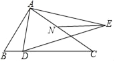
【题目】如图,在Rt△ABC中,∠BAC=90°,BC=5,AB=3,点D是线段BC上一动点,连接AD,以AD为边作△ADE∽△ABC,点N是AC的中点,连接NE,当线段NE最短时,线段CD的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A的坐标是(4,0),并且OA=OC=4OB,动点P在过A,B,C三点的抛物线上.
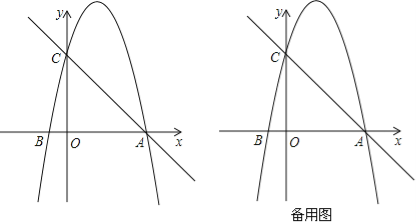
(1)求抛物线的解析式;
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直于y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂家生产一种新型电子产品,制造时每件的成本为40元,通过试销发现,销售量![]() 万件
万件![]() 与销售单价
与销售单价![]() 元
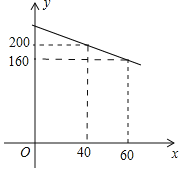
元![]() 之间符合一次函数关系,其图象如图所示.
之间符合一次函数关系,其图象如图所示.
![]() 求y与x的函数关系式;
求y与x的函数关系式;
![]() 物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x定为每件多少元时,厂家每月获得的利润
物价部门规定:这种电子产品销售单价不得超过每件80元,那么,当销售单价x定为每件多少元时,厂家每月获得的利润![]() 最大?最大利润是多少?
最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
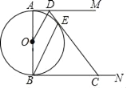
【题目】如图,⊙O的直径AB=6,AM,BN是⊙O的两条切线,点D是AM上一点,连接OD,作BE∥OD交⊙O于点E,连接DE并延长交BN于点.
(1)求证:DC是⊙O的切线;
(2)设AD=x,BC=y.求y与x的函数关系式(不要求写出自变量的取值范围)
(3)若AD=1,连接AE并延长交BC于F,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个口袋中有4个完全相同的小球,把它们分别标上数字﹣1,0,1,2,随机的摸出一个小球记录数字然后放回,在随机的摸出一个小球记录数字.求下列事件的概率:
(1)两次都是正数的概率P(A);
(2)两次的数字和等于0的概率P(B).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com