
【题目】如图,在平面直角坐标系中,A(﹣4,﹣2),B(﹣2,﹣2),C(﹣1,0).

(1)将△ABC向右平移5个单位长度,画出平移后的△A1B1C1;
(2)将△ABC绕点C旋转180°,画出旋转后的△A2B2C,并直接写出点A运动的路径长;
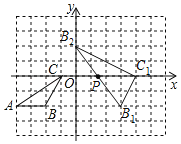
(3)请直接写出△B1C1B2的外心的坐标.
【答案】(1)如图所示,△A1B1C1即为所求;见解析;(2)如图所示,△A2B2C即为所求,见解析;点A运动的路径长为![]() π;(3)如图所示,见解析;△B1C1B2的外心P的坐标为(
π;(3)如图所示,见解析;△B1C1B2的外心P的坐标为(![]() ,0).
,0).
【解析】
(1)依据平移的方向、平移的距离即可得到平移后的△A1B1C1;
(2)依据△ABC绕点C旋转180°,即可画出旋转后的△A2B2C,再根据弧长计算公式即可得出点A运动的路径长;
(3)依据△B1C1B2为直角三角形,其外心为斜边的中点,据此可得结论.
解:(1)如图所示,△A1B1C1即为所求;
(2)如图所示,△A2B2C即为所求,点A运动的路径长为:![]() ;
;
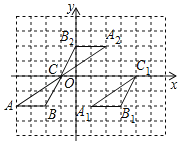
(3)如图所示,△B1C1B2的外心P的坐标为(![]() ,0).
,0).


 作业辅导系列答案
作业辅导系列答案科目:初中数学 来源: 题型:
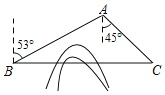
【题目】如图,C地在B地的正东方向,因有大山阻隔,由B地到C地需绕行A地,已知A地位于B地北偏东53°方向,距离B地516千米,C地位于A地南偏东45°方向.现打算打通穿山隧道,建成两地直达高铁,求建成高铁后从B地前往C地的路程.(结果精确到1千米)(参考数据:sin53°=![]() ,cos53°=
,cos53°=![]() ,tan53°=
,tan53°=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是⊙O的直径,弦CD⊥AB于H,过CD延长线上一点E作⊙O的切线交AB的延长线于F,切点为G,连接AG交CD于K.
(1)如图1,求证:KE=GE;
(2)如图2,连接CABG,若∠FGB=![]() ∠ACH,求证:CA∥FE;
∠ACH,求证:CA∥FE;
(3)如图3,在(2)的条件下,连接CG交AB于点N,若sinE=![]() ,AK=
,AK=![]() ,求CN的长.
,求CN的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线BC与⊙A相切于点C,过B作CB的垂线交⊙O于D,E两点,已知AC=![]() ,CB=a,则以BE,BD的长为两根的一元二次方程是( )
,CB=a,则以BE,BD的长为两根的一元二次方程是( )
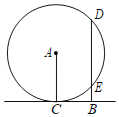
A.x2+bx+a2=0B.x2﹣bx+a2=0C.x2+bx﹣a2=0D.x2﹣bx﹣a2=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 与x轴、y轴分别交于点A、B,抛物线
与x轴、y轴分别交于点A、B,抛物线![]() 经过点A,将点B向右平移5个单位长度,得到点C,若抛物线与线段BC恰有一个公共点,则
经过点A,将点B向右平移5个单位长度,得到点C,若抛物线与线段BC恰有一个公共点,则![]() 的取值范围是____.
的取值范围是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:几个全等的正多边形依次有一边重合,排成一圈,中间可以围成一个正多边形,我们称作正多边形的环状连接。如图,我们可以看作正六边形的环状连接,中间围成一个边长相等的正六边形;若正八边形作环状连接,中间可以围的正多边形的边数为;

若正八边形作环状连接,中间可以围的正多边形的边数为________,若边长为1的正n边形作环状连接,中间围成的是等边三角形,则这个环状连接的外轮廓长为_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com