
【题目】一个不透明的盒子中有2枚黑棋,x枚白棋,这些棋子除颜色外无其他差别,现从盒中随机摸出一枚棋子(不放回),再随机摸出一枚棋子.
(1)若“摸出两枚棋子的颜色都是白色”是不可能事件,请写出符合条件的一个x值 ;
(2)当x=2时,“摸出两枚棋子的颜色相同”与“摸出两枚棋子的颜色不同”的概率相等吗?说明理由.
【答案】(1)1或0;(2)不相等.理由见解析
【解析】
(1)根据不可能事件的定义,x为小于2的正整数即可;
(2)画树状图展示所有12种等可能的结果数,再找出摸出两枚棋子的颜色相同的结果数和摸出两枚棋子的颜色不同的结果数,然后根据概率公式计算后可判定它们的概率是否相等.
解:(1)若“摸出两枚棋子的颜色都是白色”是不可能事件,则白色棋子数必须必2小,则x为1或0;
故答案为1或0;
(2)不相等.理由如下:
画树状图为:
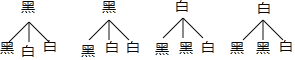
共有12种等可能的结果数,其中摸出两枚棋子的颜色相同的结果数为4,摸出两枚棋子的颜色不同的结果数为8,
所以摸出两枚棋子的颜色相同的概率![]() ,摸出两枚棋子的颜色不同的概率=
,摸出两枚棋子的颜色不同的概率=![]() =
=![]() ,
,
所以“摸出两枚棋子的颜色相同”与“摸出两枚棋子的颜色不同”的概率不相等.


 智能训练练测考系列答案
智能训练练测考系列答案 计算高手系列答案
计算高手系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中线段AB的两个端点分别在坐标轴上,点A的坐标为(1,0),将线段AB绕点A顺时针旋转90°后,点B恰好落在反比例函数y=![]() 在第一象限内的分支上的点B′,则点B的坐标为( )
在第一象限内的分支上的点B′,则点B的坐标为( )
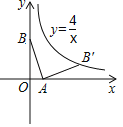
A.(0,2)B.(0,3)C.(0,4)D.(0,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
小腾遇到这样一个问题:如图1,在![]() 中,点
中,点![]() 在线段
在线段![]() 上.
上.![]() ,
,![]() ,
,![]() ,
,![]() .求
.求![]() 的长.
的长.
小腾发现,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,通过构造
,通过构造![]() ,经过推理和计算能够使问题得到解决(如图2).
,经过推理和计算能够使问题得到解决(如图2).
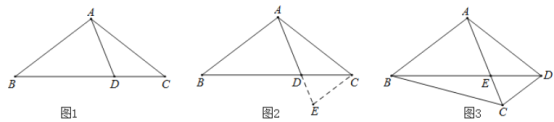
发现:![]() 的度数为 ,
的度数为 ,![]() 的长为
的长为
探究:参考小腾思考问题的方法,解决问题:
如图3,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() ,
,![]() ,求
,求![]() ,
,![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴交于点A和点B(3,0),与
轴交于点A和点B(3,0),与![]() 轴交于点C(0,3).
轴交于点C(0,3).

(1)求抛物线的解析式;
(2)若点M是抛物线在![]() 轴下方上的动点,过点M作MN//
轴下方上的动点,过点M作MN//![]() 轴交直线BC于点N,求线段MN的最大值;
轴交直线BC于点N,求线段MN的最大值;
(3)在(2)的条件下,当MN取最大值时,在抛物线的对称轴![]() 上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
上是否存在点P,使△PBN是等腰三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
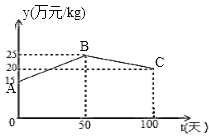
【题目】经过市场调查得知,某种商品的销售期为100天,设该商品销量单价为y(万元/kg),y与时间t(天)函数关系如下图所示,其中线段AB表示前50天销售单价y(万元/kg)与时间t(天)的函数关系;线段BC的函数关系式为y=-![]() t+m.该商品在销售期内的销量如下表:
t+m.该商品在销售期内的销量如下表:
时间t(天) | 0<t≤50 | 50<t≤100 |
销量(kg) | 200 |
|
(1)分别求出当0<t≤50和50<t≤100时y与t的函数关系式;
(2)设每天的销售收入为w(万元),则当t为何值时,w的值最大?求出最大值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() (
(![]() )的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
)的图象与x轴交于点A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(包括这两点),下列结论:
①当x>3时,y<0;
②3a+b<0;
③![]() ;
;
④![]() ;
;
其中正确的结论是( )
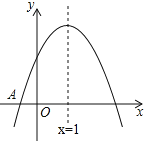
A.①③④B.①②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在△ABC中,如果正方形PQMN的边QM在BC上,顶点P,N分别在AB,AC上,那么我们称这样的正方形为“三角形内接正方形”小波同学按数学家波利亚在《怎样解题》中的方法进行操作:如图(2),任意画△ABC,在AB上任取一点P′,画正方形P′Q′M′N′,使Q′,M′在BC边上,N′在△ABC内,连结BN′并延长交AC于点N,画NM⊥BC于点M,NP⊥NM交AB于点P,PQ⊥BC于点Q,得到四边形PQMN,小波把线段BN称为“波利亚线”,请帮助小波解决下列问题:
(1)四边形PQMN是否是△ABC的内接正方形,请证明你的结论;
(2)若△ABC为等边三角形,边长BC=6,求△ABC内接正方形的边长;
(3)如图(3),若在“波利亚线”BN上截取NE=NM,连结EQ,EM.当![]() 时,猜想∠QEM的度数,并说明你的理由.
时,猜想∠QEM的度数,并说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的纸箱里有分别标有汉字“热”“爱”“祖”“国”的四个小球,除汉字不同之外,小球没有任何区别,每次摸球前先摇匀再摸球.
(1)若从中任取一个球,求摸出球上的汉字刚好是“国”字的概率;
(2)小红从中任取球,不放回,再从中任取一球,请用树状图或列表法,求小红取出的两个球上的汉字恰好能组成“爱国”或“祖国”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com