
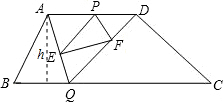
 的一动点,Q是边BC上的任意一点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F,则△PEF面积最大值是______.
的一动点,Q是边BC上的任意一点,连接AQ、DQ,过P作PE∥DQ交AQ于E,作PF∥AQ交DQ于F,则△PEF面积最大值是______.
|
|
| S△AEP |
| S△AQD |
| 3-x |
| 3 |
| S△DPF |
| S△DAQ |
| x |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 0-12 | ||
4×(-
|
| 3 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

| 2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.5个 | B.4个 | C.3个 | D.2个 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.今年3月份某周,我市每天的最高气温(单位:℃)是12,9,10,6,11,12,17,则这组数据的极差是5℃ | ||||
B.如果甲组数据的方差
| ||||
| C.在一个只装有白球和红球的袋中摸球,摸出黑球是不确定事件 | ||||
| D.了解一批电视机的使用寿命适合用抽样调查 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
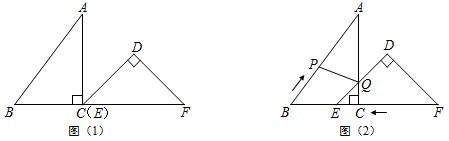
 与A,B重合),且保持DE∥BC,以DE为边,在点A的异侧作正方形DEFG.
与A,B重合),且保持DE∥BC,以DE为边,在点A的异侧作正方形DEFG.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com