练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    (1)内错角相等；

    (    )

    (2)错误的命题叫做假命题；

    (    )

    (3)如果两个角的和为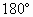，那么这两个角互为邻补角；

    (    )

    (4)两条直线相交成四个角中，如果有一个角是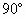，那么其它三个也都是；　　　　　　　　   

    (    )

    答案：F;T;F;T
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

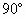    科目：初中数学 来源： 题型：

    28、阅读下面的证明过程，指出其错误．
    已知△ABC．
    求证：∠A+∠B+∠C=180度．
    证明：过A作DE∥BC，且使∠1=∠C
    ∵DE∥BC（画图）
    ∴∠2=∠B（两直线平行，内错角相等）
    ∵∠1=∠C（画图）
    ∴∠B+∠C+∠3=∠2+∠1+∠3=180°
    即∠BAC+∠B+∠C=180°

    查看答案和解析>>

    科目：初中数学 来源： 题型：

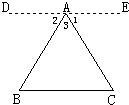
    39、如图，E点为DF上的点，B为AC上的点，∠1=∠2，∠C=∠D，那么DF∥AC，请完成它成立的理由．
    ∵∠1=∠2，∠2=∠3，∠1=∠4（
    对顶角的性质
    ）
    ∴∠3=∠4（
    等量代换
    ）
    ∴
    BD
    ∥
    CE
    ，（
    内错角相等两直线平行
    ），
    ∴∠C=∠ABD（
    两直线平行，同位角相等
    ）
    ∵∠C=∠D（
    已知
    ）
    ∴∠D=∠ABD（
    等量代换
    ）
    ∴DF∥AC（
    内错角相等，两直线平行
    ）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    26、如图，填空：
    （1）如果AB∥CD，那么∠1+
    ∠3
    =180°，
    根据是
    两直线平行，同旁内角互补
    ；
    （2）如果∠2=
    ∠D
    ，那么EF∥DG，
    根据是
    同位角相等，两直线平行
    ；
    （3）如果EF∥DG，那么∠3=
    ∠D
    ，
    根据是
    两直线平行，内错角相等
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    20、如图所示，已知直线AM、DF，C、E分别在直线AM、DF上，小华想知道∠ACE和∠DEC是否互补，但是他没有带量角器，只带了一副三角板，于是他想了这样一个办法：首先连接CF，再指出CF的中点O，然后连接EO并延长EO和直线AM相交于点B，经过测量，他发现EO=BO，因此他得出结论：∠ACE和∠DEC互补，而且他还发现BC=EF．以下是他的想法，请你填上根据．
    小华是这样想的：
    因为CF和BE相交于点O，
    根据
    对顶角相等
    得出∠COB=∠EOF；
    而O是CF的中点，那么CO=FO，又已知EO=BO，
    根据
    SAS
    得出△COB≌△FOE，
    根据
    全等三角形的对应边相等
    得出BC=EF，
    根据
    全等三角形的对应角相等
    得出∠BCO=∠F．
    既然∠BCO=∠F，根据
    内错角相等
    得出AB∥DF，
    既然AB∥DF，根据
    两直线平行，同旁内角互补
    得出∠ACE和∠DEC互补

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    8、如图所示，∠1=∠2，则
    AB
    ∥
    CD
    ，理由是
    内错角相等，两直线平行
    ．

    查看答案和解析>>

    同步练习册答案